
【题目】2015年12月16﹣18日,第二届互联网大会在浙江乌镇胜利举行,这说明我国互联网发展走到了世界的前列,尤其是电子商务.据市场调查,天猫超市在销售一种进价为每件40元的护眼台灯中发现:每月销售量y(件)与销售单价x(元)之间的函数关系如图所示.
(1)当销售单价定为50元时,求每月的销售件数;
(2)设每月获得利润为w(元),求每月获得利润w(元)关于销售单价x(元)的函数解析式;
(3)由于市场竞争激烈,这种护眼灯的销售单价不得高于75元,如果要每月获得的利润不低于8000元,那么每月的成本最少需要多少元?(成本=进价×销售量)

【答案】(1)500件;(2)w=﹣10x2+1400x﹣40000;(3)10000元.
【解析】
(1)设y=kx+b,把(40,600),(75,250)代入,列方程组即可.(2)根据利润=每件的利润×销售量,列出式子即可.(3)思想列出不等式求出x的取值范围,设成本为S,构建一次函数,利用二次函数的性质即可解决问题.
解:(1)设y=kx+b,把(40,600),(75,250)代入可得![]() ,交点
,交点![]() ,
,
∴y=﹣10x+1000,
当x=50时,y=﹣10×50+1000=500件.
(2)w=(x﹣40)(﹣10x+1000)=﹣10x2+1400x﹣40000.
(3)由题意![]() ,
,
解得60≤x≤75,
设成本为S,
∴S=40(﹣10x+1000)=﹣400x+40000,
∵﹣400<0,
∴S随x增大而减小,
∴x=75时,S有最小值=10000元.


科目:初中数学 来源: 题型:
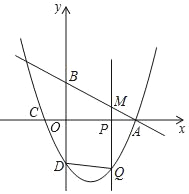
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+2分别交x轴、y轴于点A、B.点C的坐标是(﹣1,0),抛物线y=ax2+bx﹣2经过A、C两点且交y轴于点D.点P为x轴上一点,过点P作x轴的垂线交直线AB于点M,交抛物线于点Q,连结DQ,设点P的横坐标为m(m≠0).
x+2分别交x轴、y轴于点A、B.点C的坐标是(﹣1,0),抛物线y=ax2+bx﹣2经过A、C两点且交y轴于点D.点P为x轴上一点,过点P作x轴的垂线交直线AB于点M,交抛物线于点Q,连结DQ,设点P的横坐标为m(m≠0).
(1)求点A的坐标.
(2)求抛物线的表达式.
(3)当以B、D、Q,M为顶点的四边形是平行四边形时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中记载了这样一个问题,大意为:有一个善于走路的人和一个不善于走路的人.善于走路的人走100步的同时,不善于走路的人只能走60步.现不善于走路的人先走100步,善于走路的人追他,则要走多少步才能追上(两人步长相等)?设善于走路的人走x步可追上,则可列方程为____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
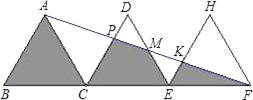
【题目】如图,△ABC、△DCE、△HEF、是三个全等的等边三角形,点B、C、E、F在同一条直线上,连接AF,与DC、DE、HE分别相交于点P、M、K,若△DPM的面积为2,则图中三个阴影部分的面积之和为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
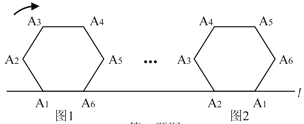
【题目】如图,将边长为![]() 的正六边形A1A2A3A4A5A6在直线
的正六边形A1A2A3A4A5A6在直线![]() 上由图1的位置按顺时针
上由图1的位置按顺时针
方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的
长为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了方便孩子入学,小王家购买了一套学区房,交首付款15万元,剩余部分向银行贷款,贷款及贷款利息按月分期还款,每月还款数相同.计划每月还款y万元,x个月还清贷款,若y是x的反比例函数,其图象如图所示:
(1)求y与x的函数解析式;
(2)若小王家计划180个月(15年)还清贷款,则每月应还款多少万元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为 24m 的篱笆,现一面利用墙(墙的最大可用长度 a 为 10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽 AB 为 xm,面积为 Sm2.
(1) 求 S 与 x 的函数关系式及 x 值的取值范围;
(2) 要围成面积为 45m2 的花圃,AB 的长是多少米?
(3) 当 AB 的长是多少米时,围成的花圃的面积最大?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.

(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
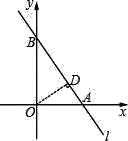
【题目】已知直线y=kx(k≠0)经过点(12,﹣5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点),则m的取值范围为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com