【题目】某超市销售一种饮料，每瓶进价为10元．经市场调查表明，当售价在12元到14元之间（含12元，14元）浮动时，日均销售y（瓶）与售价x（元）之间的关系可近似的看作一次函数，且当x＝10时，y＝500；x＝12，y＝400．
（1）求出y与x的函数关系式，并写出自变量x的取值范围．
（2）应将售价定为每瓶多少元时，所得日均毛利润最大？最大日均毛利润为多少元？（每瓶毛利润＝每瓶售价﹣每瓶进价）
【答案】（1）y＝﹣50x+1000（10≤x≤14）；（2）应将售价定为每瓶14元时，所得日均毛利润最大，最大日均毛利润为1200元．
【解析】
（1）利用待定系数法求解即可；
（2）根据“毛利润=每瓶毛利润×销售量”列出函数解析式，将其配方成顶点式后利用二次函数的性质求解可得．
（1）设y＝kx+b，
根据题意得
解得
则y＝﹣50x+1000（10≤x≤14）；
（2）设毛利润为w元，
则w＝（﹣50x+1000）（x﹣10）
＝﹣50x2+1500x﹣10000
＝﹣50（x﹣15）2+1250，
∴当x＜15时，w随x的增大而增大，
∵10≤x≤14，
∴当x＝14时，w取得最大值，最大值为1200，
答：应将售价定为每瓶14元时，所得日均毛利润最大，最大日均毛利润为1200元．
名校课堂系列答案科目：初中数学 来源： 题型：
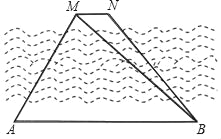
【题目】如图，在一条河的北岸有两个目标M、N，现在位于它的对岸设定两个观测点A、B．已知AB∥MN，在A点测得∠MAB＝60°，在B点测得∠MBA＝45°，AB＝600米．
(1)求点M到AB的距离；（结果保留根号）
(2)在B点又测得∠NBA＝53°，求MN的长．（结果精确到1米）
（参考数据：
≈1.732，sin53°≈0.8，cos53°≈0.6，tan53°≈1.33，cot53°≈0.75）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于x的一元二次方程x2+（2m﹣1）x+m2=0有两个实数根x1和x2．
（1）求实数m的取值范围；
（2）当x12﹣x22=0时，求m的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
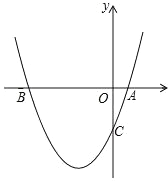
【题目】如图，已知二次函数 y＝x2+bx+c 过点 A（1，0），C（0，﹣3）
（1）求此二次函数的解析式；
（2）求△ABC 的面积；
（3）在抛物线上存在一点 P 使△ABP 的面积为 10，请求出点 P 的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，对于点P（m，n）和点Q（x，y）．给出如下定义：若
，则称点Q为点P的“伴随点”．例如：点（1，2）的“伴随点”为点（5，0）．
（1）若点Q（﹣2，﹣4）是一次函数y＝kx+2图象上点P的“伴随点”，求k的值．
（2）已知点P（m，n）在抛物线C1：y＝
上，设点P的“伴随点”Q（x，y）的运动轨迹为C2．
①直接写出C2对应的函数关系式．
②抛物线C1的顶点为A，与x轴的交点为B（非原点），试判断在x轴上是否存在点M，使得以A、B、Q、M为顶点的四边形是平行四边形？若存在，求点M的坐标；若不存在，说明理由．
③若点P的横坐标满足﹣2≤m≤a时，点Q的纵坐标y满足﹣3≤y≤1，直接写出a的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线y＝ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如表所示．
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
下列说法：①抛物线与y轴的交点为（0，6）； ②抛物线的对称轴在y轴的右侧；③抛物线一定经过点（3，0）；④在对称轴左侧，y随x增大而减小．⑤不等式ax2+（b﹣3）x+c﹣6＞0解集为﹣2＜x＜0．其中说法正确的有（ ）
A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，已知M1（3，2），N1（5，－1），线段M1N1平移至线段MN处（注：M1与M，N1与N分别为对应点）.
（1）若M（－2，5），请直接写出N点坐标.
（2）在（1）问的条件下，点N在抛物线
上，求该抛物线对应的函数解析式.
（3）在（2）问条件下，若抛物线顶点为B，与y轴交于点A，点E为线段AB中点，点C（0，m）是y轴负半轴上一动点，线段EC与线段BO相交于F，且OC︰OF=2︰
，求m的值.
（4）在（3）问条件下，动点P从B点出发，沿x轴正方向匀速运动，点P运动到什么位置时（即BP长为多少），将△ABP沿边PE折叠，△APE与△PBE重叠部分的面积恰好为此时的△ABP面积的
，求此时BP的长度.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：y=﹣10x+500，在销售过程中销售单价不低于成本价，而每件的利润不高于成本价的60%．
（1）设小明每月获得利润为w（元），求每月获得利润w（元）与销售单价x（元）之间的函数关系式，并确定自变量x的取值范围．
（2）当销售单价定为多少元时，每月可获得最大利润？每月的最大利润是多少？
（3）如果小明想要每月获得的利润不低于2000元，那么小明每月的成本最少需要多少元？（成本=进价×销售量）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商品的进价为每件40元，如果售价为每件50元，每个月可卖出210件；如果售价超过50元但不超过80元，每件商品的售价每上涨1元，则每个月少卖1件；如果售价超过80元后，若再涨价，则每涨1元每月少卖3件．设每件商品的售价为x元，每个月的销售量为y件．
（1）求y与x的函数关系式并直接写出自变量x的取值范围；
（2）设每月的销售利润为W，请直接写出W与x的函数关系式；
（3）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com