练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】函数y=ax2+1与y= （a≠0）在同一平面直角坐标系中的图象可能是（ ）
    A.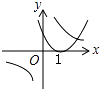
    B.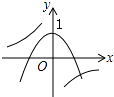
    C.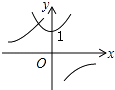
    D.

    【答案】B
    【解析】解：a＞0时，y=ax2+1开口向上，顶点坐标为（0，1）， y= 位于第一、三象限，没有选项图象符合，
    a＜0时，y=ax2+1开口向下，顶点坐标为（0，1），
    y= 位于第二、四象限，B选项图象符合．
    故选：B．
    【考点精析】掌握反比例函数的图象和二次函数的图象是解答本题的根本，需要知道反比例函数的图像属于双曲线．反比例函数的图象既是轴对称图形又是中心对称图形．有两条对称轴：直线y=x和 y=-x．对称中心是：原点；二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图甲，AB⊥BD，CD⊥BD，AP⊥PC，垂足分别为B、P、D，且三个垂足在同一直线上，我们把这样的图形叫“三垂图”．

    （1）证明：ABCD=PBPD．
    （2）如图乙，也是一个“三垂图”，上述结论成立吗？请说明理由．
    （3）已知抛物线与x轴交于点A（﹣1，0），B（3，0），与y轴交于点（0，﹣3），顶点为P，如图丙所示，若Q是抛物线上异于A、B、P的点，使得∠QAP=90°，求Q点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在同一直角坐标系中，直线y=﹣x+3与y=3x﹣5相交于C点，分别与x轴交于A、B两点．P、Q分别为直线y=﹣x+3与y=3x﹣5上的点．
    （1）求△ABC的面积；
    （2）若P、Q关于原点成中心对称，求P点的坐标；
    （3）若△QPC≌△ABC，求Q点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学校计划选购甲、乙两种图书作为“校园读书节”的奖品，已知甲种图书单价比乙种图书贵4元，用3000元购进甲种图书的数量与用2400元购进乙种图书的数量相同．
    （1）甲、乙两种图书的单价分别为多少元？
    （2）学校计划购买这两种图书共100本，请求出所需经费W（单位：元）与购买甲种图书m（单位：本）之间的函数关系式；
    （3）在（2）的条件下，要使投入的经费不超过1820元，且使购买的甲种图书的数量不少于乙种图书数量，则共有几种购买方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，AB=AC，∠BAC=60°，点E为直线AC上一点，D为直线BC上的一点，且DA=DE． 当点D在线段BC上时，如图①，易证：BD+AB=AE；
    当点D在线段CB的延长线上时，如图②、图③，猜想线段BD，AB和AE之间又有怎样的数量关系？写出你的猜想，并选择一种情况给予证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是某超市地下停车场入口的设计图，请根据图中数据计算CE的长度．（结果保留小数点后两位；参考数据：sin22°=0.3746，cos22°=0.9272，tan22°=0.4040）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1），抛物线y=﹣ x2+x+c与x轴交于A、B两点，与y轴交于点C，其中点A的坐标为（﹣2，0）．

    （1）求此抛物线的解析式；
    （2）①若点D是第一象限内抛物线上的一个动点，过点D作DE⊥x轴于E，连接CD，以OE为直径作⊙M，如图（2），试求当CD与⊙M相切时D点的坐标；
    ②点F是x轴上的动点，在抛物线上是否存在一点G，使A、C、G、F四点为顶点的四边形是平行四边形？若存在，求出点G的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学习委员统计全班50位同学对语文、数学、英语、体育、音乐五个科目最喜欢情况，所得数据用表格与条形图描述如下：

    科目

    语文

    数学

    英语

    体育

    音乐

    人数

    10

    a

    15

    3

    2


    （1）表格中a的值为；
    （2）补全条形图；
    （3）小李是最喜欢体育之一，小张是最喜欢音乐之一，计划从最喜欢体育、音乐的人中，每科目各选1人参加学校训练，用列表或树形图表示所有结果，并求小李、小张至少有1人被选上的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某数学兴趣小组想测量一棵树CD的高度，他们先在点A处测得树顶C的仰角为30°，然后沿AD方向前行10m，到达B点，在B处测得树顶C的仰角高度为60°（A、B、D三点在同一直线上）．请你根据他们测量数据计算这棵树CD的高度（结果精确到0.1m）．（参考数据： ≈1.414， ≈1.732）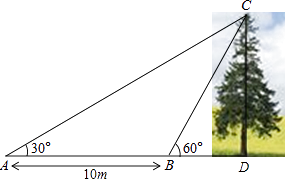

    查看答案和解析>>

    同步练习册答案