
����Ŀ��ij��˾������ij�ֲ�Ʒÿ���ɱ�Ϊ40Ԫ�����г�����������������Ϣ���ٸò�Ʒ90��������������m������ʱ�䣨��x�죩����һ�κ�����ϵ�������������±���
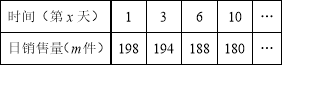
�ڸò�Ʒ90����ÿ������ۼ۸���ʱ�䣨��x�죩�Ĺ�ϵ���±���

��1����m����x��һ�κ�������ʽ��
��2�������۸ò�Ʒÿ������ΪyԪ����д��y����x�ĺ�������ʽ���������90���ڸò�Ʒ������������������������Ƕ��٣�����ʾ��ÿ����������=������������ÿ�����ۼ۸�ÿ���ɱ�����
��3���ڸò�Ʒ���۵Ĺ����У����ж���������������5400Ԫ����ֱ��д�������
���𰸡���1��m=��2x+200����2��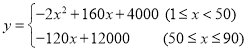 ����40�����������������������7200Ԫ����3��46��
����40�����������������������7200Ԫ����3��46��
��������
�����������1�����ݴ���ϵ�������һ�κ�������ʽ���ɣ�
��2��������ΪyԪ����1��x��50ʱ�� ![]() ����50��x��90ʱ��
����50��x��90ʱ��![]() ���ֱ���������ϵ����ֵ���Ƚϼ��ɵõ����ۣ�
���ֱ���������ϵ����ֵ���Ƚϼ��ɵõ����ۣ�
��3��ֱ��д���ڸò�Ʒ���۵Ĺ����У�����46������������5400Ԫ��
�����������1����m��x��һ�κ���������![]() ����x=1��m=198��x=3��m=194���룬�ã�
����x=1��m=198��x=3��m=194���룬�ã�![]() ����ã�
����ã�![]() ������m����x��һ�κ�������ʽΪ
������m����x��һ�κ�������ʽΪ![]() ��
��
��2�������۸ò�Ʒÿ������ΪyԪ��y����x�ĺ�������ʽΪ��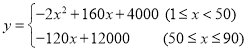 ����1��x��50ʱ��
����1��x��50ʱ��![]() =
=![]() ������2��0������x=40ʱ��y�����ֵ�����ֵ��7200��
������2��0������x=40ʱ��y�����ֵ�����ֵ��7200��
��50��x��90ʱ��![]() ������120��0����y��x�������С������x=50ʱ��y��ֵ������ֵ��6000��
������120��0����y��x�������С������x=50ʱ��y��ֵ������ֵ��6000��
������������x=40ʱ��y��ֵ������ֵ��7200������90���ڸò�Ʒ��40�����������������������7200Ԫ��
��3���ڸò�Ʒ���۵Ĺ����У�����46������������5400Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ�������
A.a4+a5��a9B.��2a2b3��2��4a4b6
C.��2a��a+3������2a2+6aD.��a+2b��2��4a2��b2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����D��E��F�ֱ���BC��AB��AC���ϣ���BE=CF��AD+EC=AB�� 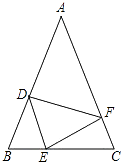
��1����֤����DEF�ǵ��������Σ�
��2������A=40��ʱ�����DEF�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����Ԫ��Ϊ����С��������һ������ͼ����������Ʒ�У������ϸ���һ�֣����������ǡ�ף��ѧ����֡������С�ף���Ķ����ǡ��¡������족�Ķ����ǡ��֡���������ƽ��չ��ͼ�����ǣ� ��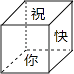
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߶�AB�Ƶ�O˳ʱ����ת90��õ��߶�A��B�䣬��ôA����2��5���Ķ�Ӧ��A��������ǣ� ��
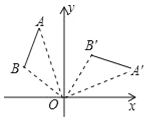
A����2��5�� B����5��2�� C����2����5�� D����5����2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ���ϣ���ʦ����������⣺
��ͼ1����Ҫ��A��B���غ�·l֮�����¹ܵ����������һ�����ʡ���ϵ���������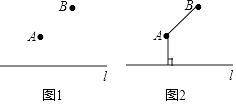
С��ͬѧ���������£�
������AB��
�ڹ���A��AC��ֱ��l�ڵ�C��
�����߶�B��A��CΪ����
��ʦ˵��С��ͬѧ�ķ�������ȷ�ģ�
��ش𣺸÷������ʡ���ϵ������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ABCD�У�E��F�ֱ��DZ�AB��CD���е㣮 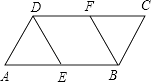
��1����֤���ı���EBFD��ƽ���ı��Σ�
��2����AD=AE=2����A=60�㣬���ı���EBFD���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ĶԽ���AC��BD���ڵ�O�������в����ж��ı���ABCD��ƽ���ı��ε������ǣ� �� 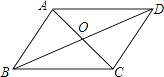
A.OA=OC��AD��BC
B.��ABC=��ADC��AD��BC
C.AB=DC��AD=BC
D.��ABD=��ADB����BAO=��DCO
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com