
【题目】
(1)(1)如图1是某个多面体的表面展开图.
①请你写出这个多面体的名称,并指出图中哪三个字母表示多面体的同一点;
②如果沿BC、GH将展开图剪成三块,恰好拼成一个矩形,那么△BMC应满足什么条件?(不必说理)
(2)如果将一个三棱柱的表面展开图剪成四块,恰好拼成一个三角形,如图2,那么该三棱柱的侧面积与表面积的比值是多少?为什么?(注:以上剪拼中所有接缝均忽略不计)
【答案】
(1)
解:①根据这个多面体的表面展开图,可得
这个多面体是直三棱柱,
点A、M、D三个字母表示多面体的同一点.
②△BMC应满足的条件是:
a、∠BMC=90°,且BM=DH,或CM=DH;
b、∠MBC=90°,且BM=DH,或BC=DH;
c、∠BCM=90°,且BC=DH,或CM=DH;
(2)
解:如图2,连接AB、BC、CA
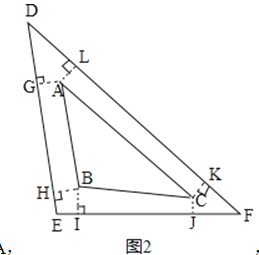
∵△DEF是由一个三棱柱表面展开图剪拼而成,
∴矩形ACKL、BIJC、AGHB为棱柱的三个侧面,
且四边形DGAL、EIBH、FKCJ须拼成与底面△ABC全等的另一个底面的三角形,
∴AC=LK,且AC=DL+FK,
∴![]() ,
,
同理,可得
![]() ,
,
∴△ABC∽△DEF,
∴![]() ,
,
即S△DEF=4S△ABC,
∴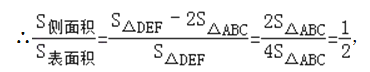 ,
,
即该三棱柱的侧面积与表面积的比值是![]() .
.
【解析】(1)①根据这个多面体的表面展开图,可得这个多面体是直三棱柱,点A、M、D三个字母表示多面体的同一点,据此解答即可.
②根据图示,要使沿BC、GH将展开图剪成三块,恰好拼成一个矩形,则△BMC应满足两个条件:△BMC中的三个内角有一个是直角;△BMC中的一条直角边和DH的长度相等,据此解答即可.
(2)首先判断出矩形ACKL、BIJC、AGHB为棱柱的三个侧面,且四边形DGAL、EIBH、FKCJ须拼成与底面△ABC全等的另一个底面的三角形,AC=LK,且AC=DL+FK,![]() ,同理,可得
,同理,可得![]() ,据此判断出△ABC∽△DEF,即可判断出S△DEF=4S△ABC;然后求出该三棱柱的侧面积与表面积的比值是多少即可.
,据此判断出△ABC∽△DEF,即可判断出S△DEF=4S△ABC;然后求出该三棱柱的侧面积与表面积的比值是多少即可.
【考点精析】利用二次函数图象的平移对题目进行判断即可得到答案,需要熟知平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减.


科目:初中数学 来源: 题型:
【题目】某中学初二年级抽取部分学生进行跳绳测试.并规定:每分钟跳90次以下的为不及格;每分钟跳90~99次的为及格;每分钟跳100~109次的为中等;每分钟跳110~119次的为良好;每分钟跳120次及以上的为优秀.测试结果整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题:
(1)参加这次跳绳测试的共有 人;
(2)补全条形统计图;
(3)在扇形统计图中,“中等”部分所对应的圆心角的度数是 °;
(4)如果该校初二年级的总人数是480人,根据此统计数据,请你估算该校初二年级跳绳成绩为“优秀”的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2的图象经过点(2,1).
(1)求二次函数y=ax2的解析式;
(2)一次函数y=mx+4的图象与二次函数y=ax2的图象交于点A(x1、y1)、B(x2、y2)两点.
①当m=![]() 时(图①),求证:△AOB为直角三角形;
时(图①),求证:△AOB为直角三角形;
②试判断当m≠![]() 时(图②),△AOB的形状,并证明; n>S扇形DOE求得即可.
时(图②),△AOB的形状,并证明; n>S扇形DOE求得即可.
(3)根据第2问,说出一条你能得到的结论.(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.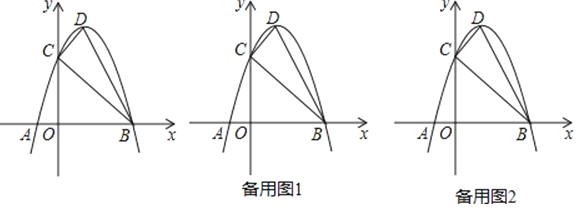
(1)填空:点C的坐标为 点D的坐标为 ;
(2)设点P的坐标为(a,0),当|PD﹣PC|最大时,求α的值并在图中标出点P的位置;
(3)在(2)的条件下,将△BCP沿x轴的正方向平移得到△B′C′P′,设点C对应点C′的横坐标为t(其中0<t<6),在运动过程中△B′C′P′与△BCD重叠部分的面积为S,求S与t之间的关系式,并直接写出当t为何值时S最大,最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点E,F分别是边AB,AC的中点,点D在边BC上.若DE=DF,AD=2,BC=6,求四边形AEDF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现正是闽北特产杨梅热销的季节,某水果零售商店分两批次从批发市场共购进杨梅40箱,已知第一、二次进货价分别为每箱50元、40元,且第二次比第一次多付款700元.
(1)设第一、二次购进杨梅的箱数分别为a箱、b箱,求a,b的值;
(2)若商店对这40箱杨梅先按每箱60元销售了x箱,其余的按每箱35元全部售完.
①求商店销售完全部杨梅所获利润y(元)与x(箱)之间的函数关系式;
②当x的值至少为多少时,商店才不会亏本.
(注:按整箱出售,利润=销售总收入﹣进货总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次初中生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题: 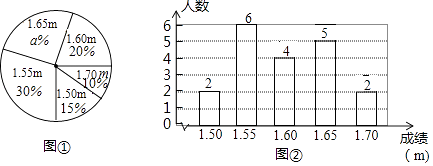
(1)①中a的值为;
(2)统计的这组初赛成绩数据的平均数、众数和中位数(结果保留小数点后两位);
(3)据这组初赛成绩,由高到低确定7人进入复赛,请直接写出初赛成绩为1.60m的运动员能否进入复赛.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com