练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．一飞机从距离地面3000米的高空测得一地面监测点的俯角是60°，那么此时飞机与监测点的距离是（　　）
    A．6000米B．1000$\sqrt{3}$米C．2000$\sqrt{3}$米D．3000$\sqrt{3}$米

    分析 根据题意可构造直角三角形，利用所给角的正弦函数即可求解．

    解答 解：如图所示：

    由题意得，∠CAB=60°，BC=3000米，
    在Rt△ABC中，∵sin∠A=$\frac{BC}{AC}$，
    ∴AC=$\frac{BC}{sinA}$=$\frac{3000}{\frac{\sqrt{3}}{2}}$=2000$\sqrt{3}$米．
    故选C．

    点评 本题考查了解直角三角形的应用，解答本题的关键是借助俯角构造直角三角形，并结合三角函数解直角三角形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    4．某商场经营某种品牌的玩具，购进时的单价是20元，根据市场调查：在一段时间内，销售单价是30元时，销售量是500件，而销售单价每上涨1元，就会少售出10件玩具．
    （1）不妨设该种品牌玩具的销售单价为x元（x＞30），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元，并把结果填写在表格中：
    销售单价（元）x（x＞30）
    销售量y（件）-10x+800 
    销售玩具获得利润w（元）-10x2+1000x-16000
    （2）在第（1）问的条件下，若商场获得了8750元销售利润，求该玩具销售单价x应定为多少元？
    （3）在第（1）问的条件下，若玩具厂规定该品牌玩具销售单价不低于32元，且商场要完成不少于400件的销售任务，求：商场销售该品牌玩具获得最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．一个四棱柱一共有12条棱．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．某市处理污水，需要铺设一条长为1000米的管道，为了尽量减少施工对交通所造成的影响，施工队进行了技术改进，因此实际施工时，每天的施工量是原计划的2倍，结果提前25天完成任务．原计划每天的施工量是多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．（1）计算：（$\frac{3x+4}{{x}^{2}-1}$-$\frac{2}{x-1}$）÷$\frac{x+2}{{x}^{2}-2x+1}$        
    （2）解方程：$\frac{3}{2}$-$\frac{1}{3x-1}$=$\frac{5}{6x-2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．如果两个相似三角形的对应中线比是$\sqrt{3}$：2，那么它们的周长比是$\sqrt{3}$：2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

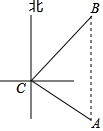    6．如图，一艘海轮位于小岛C的南偏东60°方向，距离小岛120海里的A处，该海轮从A处正北方向航行一段距离后，到达位于小岛C北偏东45°方向的B处．
    （1）求该海轮从A处到B处的航行过程中与小岛C之间的最短距离（记过保留根号）；
    （2）如果该海轮以每小时20海里的速度从B处沿BC方向行驶，求它从B处到达小岛C的航行时间（结果精确到0.1小时）．（参考数据：$\sqrt{2}$=1.41，$\sqrt{3}$=1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

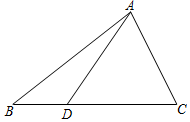    3．如图，已知点D是△ABC的边BC上一点，且BD=$\frac{1}{2}$CD，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$．
    （1）求向量$\overrightarrow{AD}$（用向量$\overrightarrow a$、$\overrightarrow b$表示）；
    （2）求作向量$\overrightarrow{AC}$在$\overrightarrow a$、$\overrightarrow b$方向上的分向量．
    （不要求写作法，但要指出所作图中表示结论的向量）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．下列多项式中，在实数范围不能分解因式的是（　　）
    A．x2+y2+2x+2yB．x2+y2+2xy-2C．x2-y2+4x+4yD．x2-y2+4y-4

    查看答案和解析>>

    同步练习册答案