Question

14．近几年“密室逃脱俱乐部”比较风靡，如图是俱乐部的通路俯视图，小张进入入口后，任选一条通道．
（1）他进A密室或B密室的可能性哪个大？请利用树状图说明理由；
（2）试求小明从右边通道进入A密室的概率．

Answer 1

分析 （1）画树状图展示所有6种等可能的结果数，再找出进A密室的结果数和进入B密室的结果数，然后计算进A密室的概率和进B密室的概率，再通过比较概率的大小判断进A密室或B密室的可能性大小；
（2）找出小明从右边通道进入A密室的结果数，然后根据概率公式计算．

解答 解：（1）画树状图为：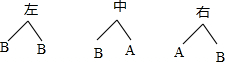

共有6种等可能的结果数，其中进A密室的结果数为2，进入B密室的结果数为4，
所以进A密室的概率=$\frac{2}{6}$=$\frac{1}{3}$，B密室的概率=$\frac{4}{6}$=$\frac{2}{3}$，
所以进A密室的可能性比进入B密室的可能性小；
（2）小明从右边通道进入A密室的概率=$\frac{1}{6}$．

点评 本题考查了列表法与树状图法：通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．