Question

4．数学上，我们常把一次函数y=2ax+b叫做二次函数y=ax²+bx+c的“切函数”，比如：二次函数y=x²-5x+6的“切函数”就是一次函数y=2x-5．
（1）若一次函数y=2x-4是二次函数y=ax²+bx+c的“切函数”，且二次函数经过点（3，0），求此二次函数的解析式及顶点坐标；
（2）己知二次函数y=αx²-6x+c与它的“切函数”y=x+b的函数图象有两个公共点A，B且AB=10$\sqrt{2}$，求a，b，c的值；（3）已知二次函数y=-x²-4x+8的“切函数”图象直线l与x釉，y轴交于C，D两点，动点P在反比例函数y=$\frac{8}{x}$（x＞0）上，求△PCD面积的最小值及此时点P的坐标．

Answer 1

分析 （1）根据二次函数y=ax²+bx+c的“切函数”的定义，可知a=1，b=-4，再把点（3，0）代入解析式即可解决问题．
（2）设A（x₁，y₁），B（x₂，y₂），由题意a=$\frac{1}{2}$，b=-6，根据AB=10$\sqrt{2}$，构建方程即可解决问题．
（3）如图，连接OP，设P（m，$\frac{8}{m}$），由S_△PCD=S_△PCO+S_△COD+S_△POD=$\frac{1}{2}$×2×$\frac{8}{m}$+$\frac{1}{2}$×4×m+$\frac{1}{2}$×2×4=$\frac{8}{m}$+2m+4=（$\sqrt{\frac{8}{m}}$-$\sqrt{2m}$）²+12，构建二次函数，利用配方法即可解决问题．

解答 解：（1）由题意a=1，b=-4，
∴抛物线解析式为y=x²-4x+c，把点（3，0）代入可得c=-3，
∴抛物线解析式为y=x²-4x-3，
∵y=x²-4x-3=（x-2）²-7，
∴抛物线的顶点坐标为（2，-7）．

（2）设A（x₁，y₁），B（x₂，y₂），由题意a=$\frac{1}{2}$，b=-6，
由$\left\{\begin{array}{l}{y=x-6}\\{y=\frac{1}{2}{x}^{2}-6x+c}\end{array}\right.$消去y得x²-14x+12+2c=0，
∴x₁+x₂=14，x₁x₂=12+2c，y₁+₂=2，y₁y₂=2c-36，
∴（x₁-x₂）²=（x₁+x₂）²-4x₁x₂=148-8c，（y₁-y₂）²=148-8c，
∵AB=10$\sqrt{2}$，
∴148-8c+148-8c=200，
∴c=6，
∴a=$\frac{1}{2}$，b=-6，c=6．

（3）如图，连接OP，设P（m，$\frac{8}{m}$），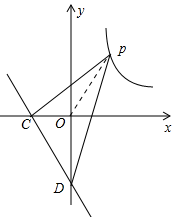

由题意直线l的解析式为y=-2x-4，
令x=0，则y=-4，令y=0，则x=-2，
∴C（-2，0），D（0．-4），
∵S_△PCD=S_△PCO+S_△COD+S_△POD=$\frac{1}{2}$×2×$\frac{8}{m}$+$\frac{1}{2}$×4×m+$\frac{1}{2}$×2×4=$\frac{8}{m}$+2m+4=（$\sqrt{\frac{8}{m}}$-$\sqrt{2m}$）²+12，
∴当$\sqrt{\frac{8}{m}}$=$\sqrt{2m}$时，△PCD的面积有最小值，最小值为12．
∴m=2，此时P（2，4）．
∴当P（2，4）时，△PCD的面积最小，最小值为12．

点评 本题考查二次函数的综合题、待定系数法、一元二次方程的根与系数的关系等知识，解题的关键是灵活应用这些知识解决问题，学会利用参数解决问题，学会构建二次函数，利用二次函数的性质解决问题，属于中考压轴题．