
【题目】如图:AD是正△ABC的高,O是AD上一点,⊙O经过点D,分别交AB、AC于E、F
(1)求∠EDF的度数;
(2)若AD=6![]() ,求△AEF的周长;
,求△AEF的周长;
(3)设EF、AD相较于N,若AE=3,EF=7,求DN的长.
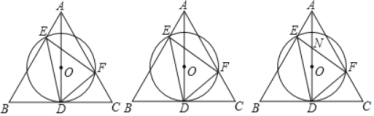
【答案】(1)60°;⑵18;⑶DN=![]()
【解析】
(1)作OI⊥AB于I,OJ⊥AC于J,连接OE,OF,可得△OIE≌△OJF(HL),∠EOF=120°,
可得∠EDF的度数;
(2)设AD与圆O交于点G,连接FG,AD是正△ABC的高,∠B=∠C=60°,CD=BD, GD是圆O的直径,由圆与正三角形的对称性,可得∠BED=∠ FED, 作DK⊥AB,DL⊥AC,DM⊥EF,可得DK=DL,可得△EKD≌EFD与△DMF≌△DLF,可得△AEF的周长=AF+AE+EF=2AL,可得答案.
(3)过E点AC的垂线,长为![]() ,过E点做AD的垂线,长为
,过E点做AD的垂线,长为![]() ,过F做AD的垂线,长为
,过F做AD的垂线,长为![]() ,设AC=x,
,设AC=x,![]() =
=![]() =
=![]() ,AF=
,AF=![]() -10,FC=10-
-10,FC=10-![]() ,EB=x-3,BD=DC=
,EB=x-3,BD=DC=![]() ,由△FDC∽△DEB,可得
,由△FDC∽△DEB,可得![]() ,代入可得x的值,由
,代入可得x的值,由![]() =
=![]() ,可得AN,可求得DN.
,可得AN,可求得DN.
解:(1)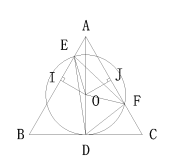
AD是正△ABC的高,∴∠BAC=60°,AD平分∠BAC,
∴∠BAD=∠CAD=30°,
作OI⊥AB于I,OJ⊥AC于J,连接OE,OF,∴OI=OJ,
∴△OIE≌△OJF(HL),∴∠IOE=∠JOF
∴∠EOF=∠EOJ+∠FOJ=∠EOJ+∠IOE=∠IOJ=120°,
∴∠EDF=![]() ∠EOF=60°
∠EOF=60°
⑵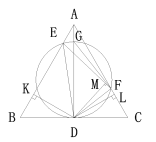
设AD与圆O交于点G,连接FG,AD是正△ABC的高,∠B=∠C=60°,CD=BD, GD是圆O的直径,由圆与正三角形的对称性,可得∠BED=∠ FED, 作DK⊥AB,DL⊥AC,DM⊥EF,可得DK=DL
![]() ∠BED=∠ FED,DK⊥AB, DM⊥EF,ED=ED
∠BED=∠ FED,DK⊥AB, DM⊥EF,ED=ED
![]() △EKD≌EFD,
△EKD≌EFD, ![]() EK=EM,DK=DM,
EK=EM,DK=DM,
在△DMF与△DLF中,
DK=DM=DL, DL⊥AC,DM⊥EF,
![]() △DMF≌△DLF,
△DMF≌△DLF, ![]() MF=FL
MF=FL
易得:AK=AL,AL=![]() AC=9
AC=9
△AEF的周长=AF+AE+EF=2AL,AL=9,∴![]() =18=
=18=![]()
⑶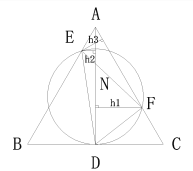
过E点AC的垂线,长为![]() ,过E点做AD的垂线,长为
,过E点做AD的垂线,长为![]() ,过F做AD的垂线,长为
,过F做AD的垂线,长为![]() ,
,
设AC=x,![]() =
=![]() =
=![]() ,AF=
,AF=![]() -10,FC=10-
-10,FC=10-![]() ,EB=x-3,BD=DC=
,EB=x-3,BD=DC=![]() ,
,
由△FDC∽△DEB,可得![]() ,代入得:
,代入得:
![]() ,解得:
,解得:![]() =12,
=12,![]() =
=![]() (舍去),
(舍去),
AF=![]() -10=8,AD=
-10=8,AD=![]() =
=![]() ,
,
![]() =
=![]()
可得AN=![]()
![]() DN=
DN=![]()


科目:初中数学 来源: 题型:
【题目】将号码分别为1,2,3,…,9的九个小球放入一个袋中,这些小球仅号码不同,其余完全相同,甲从袋中摸出一个球,号码为a,放回后乙再摸出一个球,号码为b,则使不等式![]() 成立的事件发生的概率为( )
成立的事件发生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
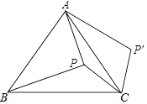
【题目】如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P'C,连接AP',则sin∠PAP'的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,点E在AD边上运动,且不与点A和点D重合,连结CE,过点C作CF⊥CE交AB的延长线于点F,EF交BC于点G.
(1)求证:△CDE≌△CBF;
(2)当DE=![]() 时,求CG的长;
时,求CG的长;
(3)连结AG,在点E运动过程中,四边形CEAG能否为平行四边形?若能,求出此时DE的长;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在推进城乡义务教育均衡发展工作中,我市某区政府通过公开招标的方式为辖区内全部乡镇中学采购了某型号的学生用电脑和教师用笔记本电脑,其中,A乡镇中学更新学生用电脑110台和教师用笔记本电脑32台,共花费30.5万元;B乡镇中学更新学生电脑55台和教师用笔记本电脑24台,共花费17.65万元.
(1)求该型号的学生用电脑和教师用笔记本电脑单价分别是多少万元?
(2)经统计,全部乡镇中学需要购进的教师用笔记本电脑台数比购进的学生用电脑台数的![]() 少90台,在两种电脑的总费用不超过预算438万元的情况下,至多能购进的学生用电脑和教师用笔记本电脑各多少台?
少90台,在两种电脑的总费用不超过预算438万元的情况下,至多能购进的学生用电脑和教师用笔记本电脑各多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论中,正确结论的有( )个.
①b2﹣4ac>0;②abc>0;③8a+c>0;④9a+3b+c<0.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于点C,点M为抛物线的顶点,且OC=OB.
(1)求抛物线的解析式.
(2)若抛物线上有一点P,连PC交线段BM于Q点,且S△BPQ=S△CMQ,求P点的坐标.
(3)把抛物线沿x轴正半轴平移n个单位,使平移后的抛物线交直线BC于E、F两点,且E、F关于点B对称,求n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
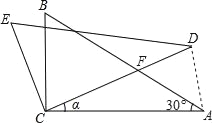
【题目】如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于F,连接AD,△ADF是等腰三角形旋转角α度数为( )
A. 20° B. 40° C. 20°或40° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=![]() , AD=4.
, AD=4.
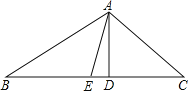
(1)求BC的长;
(2)求tan∠DAE的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com