
【题目】如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
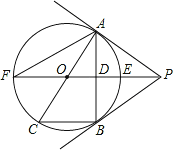
(1)求证:直线PA为⊙O的切线;
(2)试探究线段EF、OD、OP之间的等量关系,并加以证明;
(3)若BC=6,tan∠F=![]() ,求cos∠ACB的值和线段PE的长.
,求cos∠ACB的值和线段PE的长.
【答案】(1)证明见解析(2)EF2=4ODOP,证明见解析(3)![]() ,
,![]()
【解析】解:(1)连接OB,
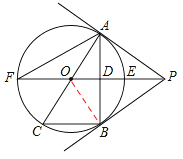
∵PB是⊙O的切线,∴∠PBO=90°。
∵OA=OB,BA⊥PO于D,
∴AD=BD,∠POA=∠POB。
又∵PO=PO,∴△PAO≌△PBO(SAS)。
∴∠PAO=∠PBO=90°。∴直线PA为⊙O的切线。
(2)EF2=4ODOP。证明如下:
∵∠PAO=∠PDA=90°,∴∠OAD+∠AOD=90°,∠OPA+∠AOP=90°。
∴∠OAD=∠OPA。∴△OAD∽△OPA,∴![]() ,即OA2=ODOP。
,即OA2=ODOP。
又∵EF=2OA,∴EF2=4ODOP。
(3)∵OA=OC,AD=BD,BC=6,∴OD=![]() BC=3(三角形中位线定理)。
BC=3(三角形中位线定理)。
设AD=x,
∵tan∠F=![]() ,∴FD=2x,OA=OF=2x﹣3。
,∴FD=2x,OA=OF=2x﹣3。
在Rt△AOD中,由勾股定理,得(2x﹣3)2=x2+32,
解得,x1=4,x2=0(不合题意,舍去)。∴AD=4,OA=2x﹣3=5。
∵AC是⊙O直径,∴∠ABC=90°。
又∵AC=2OA=10,BC=6,∴cos∠ACB=![]() 。
。
∵OA2=ODOP,∴3(PE+5)=25。∴PE=![]() 。
。
(1)连接OB,根据垂径定理的知识,得出OA=OB,∠POA=∠POB,从而证明△PAO≌△PBO,然后利用全等三角形的性质结合切线的判定定理即可得出结论。
(2)先证明△OAD∽△OPA,由相似三角形的性质得出OA与OD、OP的关系,然后将EF=2OA代入关系式即可。
(3)根据题意可确定OD是△ABC的中位线,设AD=x,然后利用三角函数的知识表示出FD、OA,在Rt△AOD中,由勾股定理解出x的值,从而能求出cos∠ACB,再由(2)可得OA2=ODOP,代入数据即可得出PE的长。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商场将每件进价为![]() 元的某种商品原来按每件
元的某种商品原来按每件![]() 元出售,一天可售出
元出售,一天可售出![]() 件.后来经过市场调查,发现这种商品单价每降低
件.后来经过市场调查,发现这种商品单价每降低![]() 元,其销量可增加
元,其销量可增加![]() 件.
件.
![]() 求商场经营该商品原来一天可获利润多少元?
求商场经营该商品原来一天可获利润多少元?
![]() 若商场经营该商品一天要获利润
若商场经营该商品一天要获利润![]() 元,并让顾客得到实惠,则每件商品应降价多少元?
元,并让顾客得到实惠,则每件商品应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+(m+4)x-2(m+6)(m是常数,m≠-8)与x轴有两个不同的交点A、B,点A、点B关于直线x=1对称,抛物线的顶点为C.
(1)此抛物线的解析式;
(2)求点A、B、C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个木制的棱长为3的正方体的表面涂上颜色,将它的棱三等分,然后从等分点把正方体锯开,得到27个棱长为l的小正方体,将这些小正方体充分混合后,装入口袋,从这个口袋中任意取出一个小正方体,则这个小正方体的表面恰好涂有两面颜色的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点C在半圆O上,AB=5cm,AC=4cm.D是弧BC上的一个动点(含端点B,不含端点C),连接AD,过点C作CE⊥AD于E,连接BE,在点D移动的过程中,BE的取值范围是____.
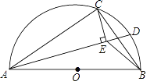
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象的一支位于第一象限.
的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求w的取值范围;
(2)点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,点C与点A关于原点O对称,若△ABC的面积为4,求w的值.
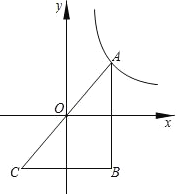
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是梯形ABCD的内切圆,AB∥DC,E、M、F、N分别是边AB、BC、CD、DA上的切点.
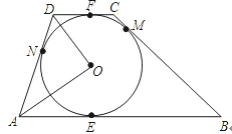
(1)求证:AB+CD=AD+BC
(2)求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字1,2,3;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,﹣3,现从甲袋中随机摸出一个小球,将标有的数字记录为x,再从乙袋中随机摸出一个小球,将标有的数字记录为y,确定点M的坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在反比例函数y=![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com