【题目】已知抛物线y=x2+(m+4)x-2(m+6)(m是常数，m≠-8)与x轴有两个不同的交点A、B，点A、点B关于直线x=1对称，抛物线的顶点为C.
（1）此抛物线的解析式；
（2）求点A、B、C的坐标.
【答案】（1）y=x2-2x；（2）（0，0），（2，0），（1，-1）．
【解析】
试题（1）根据已知条件知，该抛物线的对称轴是x=1，然后利用抛物线对称轴方程列出关于m的方程
，则易求m的值；
（2）根据（1）中的函数解析式知，分别求当x=0，y的值；当y=0时，x的值．
试题解析：：（1）∵抛物线
（m为常数，m≠-8））的对称轴为
，而抛物线与x轴有两个不同的交点A、B，点A、点B关于直线x=1对称，
∴，解得m=-6.
∴所求抛物经的解析式为y=x2-2x.
（2）当y=0时，x2-2x=0，解得x1=0，x2=2.
又y=x2-2x=（x-1）2-1，
∴点A、B、C的坐标．分别为（0，0），（2，0），（1，-1）．
科目：初中数学 来源： 题型：
【题目】如图，将△ABC沿BC方向平移2cm得到△DEF，若△ABC的周长为16cm，則四辺形ABFD的周长为( )
A. 16cmB. 18cmC. 20cmD. 22cm
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（本题6分）甲、乙两人进行摸牌游戏．现有三张形状大小完全相同的牌，正面分别标有数字2，3，5．将三张牌背面朝上，洗匀后放在桌子上．
（1）甲从中随机抽取一张牌，记录数字后放回洗匀，乙再随机抽取一张．请用列表法或画树状图的方法，求两人抽取相同数字的概率；
（2）若两人抽取的数字和为2的倍数，则甲获胜；若抽取的数字和为5的倍数，则乙获胜．这个游戏公平吗？请用概率的知识加以解释．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利44元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出5件。若商场平均每天要盈利1600元，每件衬衫应降价多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
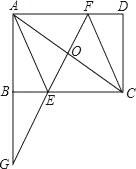
【题目】如图，矩形ABCD中，O是对角线AC的中点，延长AB到G，使BG＝AB，连接GO并延长，交BC于E，交AD于F，且AC＝2AB，连接AE、CF．求证：四边形AECF是菱形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，小正方形网格的边长为1个单位长度，△ABC的三个顶点的坐标分别为A(﹣3，4)，B(﹣5，2)，C(﹣2，1)．
(1)画出△ABC绕原点O逆时针方向旋转90°得到的△A'B'C'；并直接写出点A'，B'，C'的坐标：A' ，B' ，C' ．
(2)在(1)的条件下，求在旋转的过程中，点A所经过的路径长，(结果保留π)
查看答案和解析>>
科目：初中数学 来源： 题型：
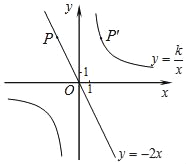
【题目】如图，已知直线y＝﹣2x经过点P（﹣2，a），点P关于y轴的对称点P′在反比例函数y＝
（k≠0）的图象上．
（1）求反比例函数的解析式；
（2）直接写出当y＜4时x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，PB为⊙O的切线，B为切点，直线PO交⊙于点E、F，过点B作PO的垂线BA，垂足为点D，交⊙O于点A，延长AO与⊙O交于点C，连接BC，AF．
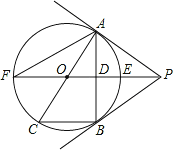
（1）求证：直线PA为⊙O的切线；
（2）试探究线段EF、OD、OP之间的等量关系，并加以证明；
（3）若BC=6，tan∠F=
，求cos∠ACB的值和线段PE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线 y＝
x2﹣2x的顶点是A，与x轴相交于点B、C两点（点B在点C的左侧）．
（1）求A、B、C的坐标；
（2）直接写出当y＜0时x的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com