
ЁОЬтФПЁПФГЪ§бЇЛюЖЏаЁзщдквЛДЮЛюЖЏжаЃЌЖдвЛИіЪ§зжЮЪЬтзїШчЯТбаОПЃК
ЃЈЮЪЬтЗЂЯжЃЉШчЭМЂйЃЌдкЕШБпШ§НЧаЮABCжаЃЌЕуMЪЧBCЩЯШЮвтвЛЕуЃЌСЌНгAMЃЌвдAMЮЊБпзїЕШБпЁїAMNЃЌСЌНгCNЃЌХаЖЯCNКЭABЕФЮЛжУЙиЯЕЃКЁЁ ЁЁЃЛ
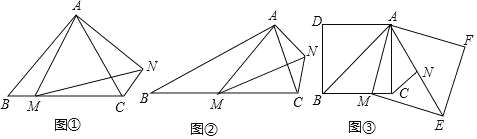
ЃЈБфЪНЬНОПЃЉШчЭМЂкЃЌдкЕШбќШ§НЧаЮABCжаЃЌBAЃНBCЃЌЕуMЪЧBCБпЩЯШЮвтвЛЕуЃЈВЛКЌЖЫЕуBЃЌCЃЉЃЌСЌНгAMЃЌвдAMЮЊБпзїЕШбќШ§НЧаЮAMNЃЌЪЙЖЅНЧЁЯAMNЃНЁЯABCЃЌMAЃНMNЃЌСЌНгCNЃЌЪдЬНОПЁЯABCгыЁЯACNЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЃЈНтОіЮЪЬтЃЉШчЭМЂлЃЌдке§ЗНаЮADBCжаЃЌЕуMЮЊBCБпЩЯвЛЕуЃЌвдAMЮЊБпзїе§ЗНаЮAMEFЃЌЕуNЮЊе§ЗНаЮAMEFЕФжааФЃЌСЌНгCNЃЌШєе§ЗНаЮADBCЕФБпГЄЮЊ8ЃЌCNЃН![]() ЃЌжБНгаДГіе§ЗНаЮAMEFЕФБпГЄЃЎ
ЃЌжБНгаДГіе§ЗНаЮAMEFЕФБпГЄЃЎ
ЁОД№АИЁПЁОЮЪЬтЗЂЯжЁПжЄУїМћНтЮіЃЛ
ЁОБфЪНЬНОПЁПЁЯABCЃНЁЯACNЃЌРэгЩМћНтЮіЃЛ
ЁОНтОіЮЪЬтЁПе§ЗНаЮAMEFЕФБпГЄЮЊ10ЃЎ
ЁОНтЮіЁП
ЁОЮЪЬтЗЂЯжЁП
ИљОнЁїABCЃЌЁїAMNЮЊЕШБпШ§НЧаЮЃЌЕУЕНAB=ACЃЌAM=ANЧвЁЯBAC=ЁЯMAN=60ЁуДгЖјЕУЕНЁЯBAC-ЁЯCAM=ЁЯMAN-ЁЯCAMЃЌМДЁЯBAM=ЁЯCANЃЌжЄУїЁїBAMЁеЁїCANЃЌМДПЩЕУЕНBM=CNЃЎ
ЁОБфЪНЬНОПЁПИљОнЁїABCЃЌЁїAMNЮЊЕШбќШ§НЧаЮЃЌЕУЕНABЃКBC=1ЃК1ЧвЁЯABC=ЁЯAMNЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪЕУЕН![]() ЃЌРћгУЕШбќШ§НЧаЮЕФаджЪЕУЕНЁЯBAC=ЁЯMANЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪМДПЩЕУЕННсТлЃЛ
ЃЌРћгУЕШбќШ§НЧаЮЕФаджЪЕУЕНЁЯBAC=ЁЯMANЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪМДПЩЕУЕННсТлЃЛ
ЁОНтОіЮЪЬтЁПИљОне§ЗНаЮЕФаджЪЕУЕНЁЯABC=ЁЯBAC=45ЁуЃЌЁЯMAN=45ЁуЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪЕУГі![]() ЃЌЕУЕНBM=2ЃЌCM=6ЃЌдйИљОнЙДЙЩЖЈРэМДПЩЕУЕНД№АИЃЎ
ЃЌЕУЕНBM=2ЃЌCM=6ЃЌдйИљОнЙДЙЩЖЈРэМДПЩЕУЕНД№АИЃЎ
НтЃКЁОЮЪЬтЗЂЯжЁПCNЁЮABЃЌ
ЁпЁїABCгыЁїMNЪЧЕШБпШ§НЧаЮЃЌ
ЁрABЃНACЃЌAMЃНANЃЌЁЯBACЃНЁЯMANЃН60ЁуЃЌ
ЁрЁЯBAMЃНЁЯCANЃЌ
дкЁїABMгыЁїACNжаЃЌ ЃЌ
ЃЌ
ЁрЁїABMЁеЁїACNЃЌ
ЁрЁЯBЃНЁЯACNЃН60ЁуЃЌ
ЁпЁЯANC+ЁЯACN+ЁЯCANЃНЁЯANC+60Ёу+ЁЯCANЃН180ЁуЃЌ
ЁрЁЯANC+ЁЯMAN+ЁЯBAMЃНЁЯANC+60Ёу+ЁЯCANЃНЁЯBAN+ЁЯANCЃН180ЁуЃЌ
ЁрCNЁЮABЃЛ
ЁОБфЪНЬНОПЁП
ЁЯABCЃНЁЯACNЃЌ
РэгЩЃКЁп![]() ЃН1ЧвЁЯABCЃНЁЯAMNЃЌ
ЃН1ЧвЁЯABCЃНЁЯAMNЃЌ
ЁрЁїABCЁЋЁїAMNЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпABЃНBCЃЌ
ЁрЁЯBACЃН![]() ЃЌ
ЃЌ
ЁпAMЃНMN
ЁрЁЯMANЃН![]() ЃЌ
ЃЌ
ЁпЁЯBЃНЁЯAMNЃЌ
ЁрЁЯBAMЃНЁЯCANЃЌ
ЁрЁїABMЁЋЁїACNЃЌ
ЁрЁЯABCЃНЁЯACNЃЛ
ЁОНтОіЮЪЬтЁП
ЁпЫФБпаЮADBCЃЌAMEFЮЊе§ЗНаЮЃЌ
ЁрЁЯABCЃНЁЯBACЃН45ЁуЃЌЁЯMANЃН45ЁуЃЌ
ЁрЁЯBACЉЁЯMACЃНЁЯMANЉЁЯMAC
МДЁЯBAMЃНЁЯCANЃЌ
Ёп![]()
Ёр![]() ЃЌ
ЃЌ
ЁрЁїABMЁЋЁїACN
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
Ёр![]() ЃЌ
ЃЌ
ЁрBMЃН2ЃЌ
ЁрCMЃН6
дкRtЁїAMCЃЌACЃН8ЃЌCMЃН6ЃЌ
![]()
Д№ЃКе§ЗНаЮAMEFЕФБпГЄЮЊ10ЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
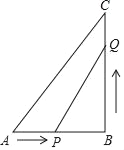
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкЁїABCжаЃЌЁЯB=90ЁуЃЌAB=5cmЃЌBC=7cmЃЎЕуPДгЕуAПЊЪМбиABБпЯђЕуBвд1cm/sЕФЫйЖШвЦЖЏЃЌЕуQДгЕуBПЊЪМбиBCБпЯђЕуCвд2cm/sЕФЫйЖШвЦЖЏЃЎ
ЃЈ1ЃЉШчЙћPЃЌQЗжБ№ДгAЃЌBЭЌЪБГіЗЂЃЌФЧУДМИУыКѓЃЌЁїPBQЕФУцЛ§ЕШгк6cm2ЃП
ЃЈ2ЃЉдкЃЈ1ЃЉжаЃЌЁїPQBЕФУцЛ§ФмЗёЕШгк8cm2ЃПЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дкЁїACDжа,ЁЯACDЃН90Ёу,ACЃНb,CDЃНa,ADЃНc,ЕуBдкCDЕФбгГЄЯпЩЯ
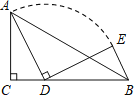
(1)ЧѓжЄ:ЙигкxЕФвЛдЊЖўДЮЗНГЬ![]() БигаЪЕЪ§Иљ
БигаЪЕЪ§Иљ
(2)ЕБbЃН3,CBЃН5ЪБ.НЋЯпЖЮADШЦЕуDЫГЪБеыа§зЊ90Ёу,ЕУЕНЯпЖЮDE,СЌНгBE,дђЕБaЕФжЕЮЊЖрЩйЪБ,ЯпЖЮBEЕФГЄзюЖЬ,зюЖЬГЄЖШЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕчзгГЇЩЬЭЖВњвЛжжаТаЭЕчзгВњЦЗЃЌУПМўжЦдьГЩБОЮЊ18дЊЃЌЪдЯњЙ§ГЬжаЗЂЯжЃЌУПдТЯњЪлСПyЃЈЭђМўЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉжЎМфЕФЙиЯЕПЩвдНќЫЦЕиПДзївЛДЮКЏЪ§![]() ЃЈРћШѓ=ЪлМлЉжЦдьГЩБОЃЉЃЎ
ЃЈРћШѓ=ЪлМлЉжЦдьГЩБОЃЉЃЎ
ЃЈ1ЃЉаДГіУПдТЕФРћШѓwЃЈЭђдЊЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЕБЯњЪлЕЅМлЮЊЖрЩйдЊЪБЃЌГЇЩЬУПдТФмЛёЕУ350ЭђдЊЕФРћШѓЃП
ЃЈ3ЃЉЕБЯњЪлЕЅМлЮЊЖрЩйдЊЪБЃЌГЇЩЬУПдТФмЛёЕУзюДѓРћШѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвбжЊе§БШР§КЏЪ§yЃН![]() xЕФЭМЯѓгыЗДБШР§КЏЪ§yЃН
xЕФЭМЯѓгыЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓНЛгкAЃЈaЃЌЃ2ЃЉЃЌBСНЕуЃЎ
ЕФЭМЯѓНЛгкAЃЈaЃЌЃ2ЃЉЃЌBСНЕуЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФБэДяЪНКЭЕуBЕФзјБъЃЛ
ЃЈ2ЃЉPЪЧЕквЛЯѓЯоФкЗДБШР§КЏЪ§ЭМЯѓЩЯвЛЕуЃЌЙ§ЕуPзїyжсЕФЦНааЯпЃЌНЛжБЯпABгкЕуCЃЌСЌНгPOЃЌШєЁїPOCЕФУцЛ§ЮЊ3ЃЌЧѓЕуPЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
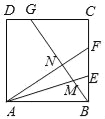
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDжаЃЌBE=EF=FCЃЌCG=2GDЃЌBGЗжБ№НЛAEЃЌAFгкMЃЌNЃЎЯТСаНсТлЃКЂйAFЁЭBGЃЛЂкBN=![]() NFЃЛЂл
NFЃЛЂл![]() ЃЛЂмSЫФБпаЮCGNF=
ЃЛЂмSЫФБпаЮCGNF=![]() SЫФБпаЮANGDЃЎЦфжае§ШЗЕФНсТлЕФађКХЪЧ ЃЎ
SЫФБпаЮANGDЃЎЦфжае§ШЗЕФНсТлЕФађКХЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈ:ЂйЮЛЫЦЭМаЮЖМЯрЫЦЃЛЂкЮЛЫЦЭМаЮЖМЪЧЦНвЦКѓдйЗХДѓ(ЛђЫѕаЁ)ЕУЕНЃЛЂлжБНЧШ§НЧаЮаББпЩЯЕФжаЯпгыаББпЕФБШЮЊ1:2ЃЛЂмСНИіЯрЫЦЖрБпаЮЕФУцЛ§БШЮЊ4:9ЃЌдђжмГЄЕФБШЮЊ16:81жаЃЌе§ШЗЕФга( )

A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
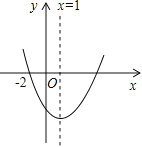
ЁОЬтФПЁПШчЭМЫљЪОЕФХзЮяЯпЪЧЖўДЮКЏЪ§![]() ЃЈaЁй0ЃЉЕФЭМЯѓЃЌдђЯТСаНсТлЃКЂйabcЃО0ЃЛЂкb+2a=0ЃЛЂлХзЮяЯпгыxжсЕФСэвЛИіНЛЕуЮЊЃЈ4ЃЌ0ЃЉЃЛЂмa+cЃОbЃЛЂн3a+cЃМ0ЃЎЦфжае§ШЗЕФНсТлга
ЃЈaЁй0ЃЉЕФЭМЯѓЃЌдђЯТСаНсТлЃКЂйabcЃО0ЃЛЂкb+2a=0ЃЛЂлХзЮяЯпгыxжсЕФСэвЛИіНЛЕуЮЊЃЈ4ЃЌ0ЃЉЃЛЂмa+cЃОbЃЛЂн3a+cЃМ0ЃЎЦфжае§ШЗЕФНсТлга
A. 5Иі B. 4Иі C. 3Иі D. 2Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
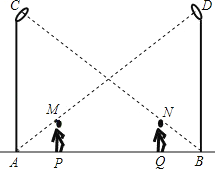
ЁОЬтФПЁПШчЭМЃЌЭѕЛЊЭЌбЇдкЭэЩЯгЩТЗЕЦACзпЯђТЗЕЦBDЃЌЕБЫћзпЕНЕуPЪБЃЌЗЂЯжЩэКѓЫћгАзгЕФЖЅВПИеКУНгДЅЕНТЗЕЦACЕФЕзВПЃЌЕБЫћЯђЧАдйВНаа12mЕНДяQЕуЪБЃЌЗЂЯжЩэЧАЫћгАзгЕФЖЅВПИеКУНгДЅЕНТЗЕЦBDЕФЕзВПЃЎвбжЊЭѕЛЊЭЌбЇЕФЩэИпЪЧ1.6mЃЌСНИіТЗЕЦЕФИпЖШЖМЪЧ9.6mЃЎ
ЃЈ1ЃЉЧѓСНИіТЗЕЦжЎМфЕФОрРыЃЛ
ЃЈ2ЃЉЕБЭѕЛЊЭЌбЇзпЕНТЗЕЦBDДІЪБЃЌЫћдкТЗЕЦACЯТЕФгАзгГЄЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com