

| PH |
| PA |
| ||
| 2 |
| ||
| 2 |
| 3 |
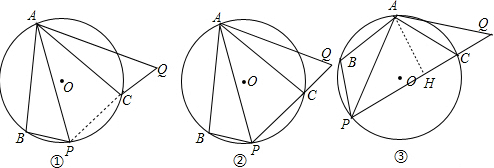 证明:连结PC,如图①,
证明:连结PC,如图①,| 3 |
| PH |
| PA |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
| 2 |
| x |
| A、4个 | B、3个 | C、2个 | D、1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 品牌 价格 |
甲 | 乙 |
| 进价(元/部) | 4000 | 2500 |
| 售价(元/部) | 4300 | 3000 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
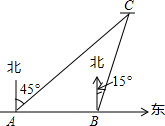 2014年3月8日凌晨,马来西亚航空公司吉隆坡飞北京的MH370航班在起飞一个多小时后在雷达上消失,至今没有被发现踪迹.飞机上有239名乘客,其中154名是中国同胞.中国政府启动了全面应急和搜救机制,派出多艘中国舰船在相关海域进行搜救.如图,某日在南印度洋海域有两艘自西向东航行的搜救船A,B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两船同时测得在A的东北方向,B的北偏东15°方向有疑似物C,求此时疑似物C与搜救船A,B的距离各是多少(结果保留根号)
2014年3月8日凌晨,马来西亚航空公司吉隆坡飞北京的MH370航班在起飞一个多小时后在雷达上消失,至今没有被发现踪迹.飞机上有239名乘客,其中154名是中国同胞.中国政府启动了全面应急和搜救机制,派出多艘中国舰船在相关海域进行搜救.如图,某日在南印度洋海域有两艘自西向东航行的搜救船A,B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两船同时测得在A的东北方向,B的北偏东15°方向有疑似物C,求此时疑似物C与搜救船A,B的距离各是多少(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com