
【题目】如图,已知:梯形ABCD中,AD∥BC,E为AC的中点,连接DE并延长交BC于点F,连接AF.
(1)求证:AD=CF;
(2)在原有条件不变的情况下,请你再添加一个条件(不再增添辅助线),使四边形AFCD成为菱形,并说明理由.
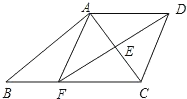
【答案】(1)见解析;(2)添加DA=DC,见解析
【解析】
(1)根据AD∥BC证得∠DAE=∠FCE,∠ADE=∠EFC,根据E为AC的中点得到AE=CE,再利用AAS证得△DEA≌△FEC即可得到AD=CF;
(2)若四边形AFCD成为菱形,则应证四边形AFCD是平行四边形,因而加一组邻边相等即可,如:DA=DC.
(1)证明:在△DEA和△FEC中,
∵AD∥BC,
∴∠DAE=∠FCE,∠ADE=∠EFC.
又∵E为AC的中点,
∴AE=CE.
∴△DEA≌△FEC.
∴AD=CF.
(2)添加DA=DC.
证明:∵AD∥BC,
又∵AD=CF,
∴四边形AFCD为平行四边形.
又∵DA=DC,
∴四边形AFCD为菱形.


科目:初中数学 来源: 题型:
【题目】二次函数图象的顶点在原点![]() ,经过点
,经过点![]() 点
点![]() 在
在![]() 轴上,直线
轴上,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.

(1)求二次函数的解析式;
(2)点![]() 是抛物线上的点,过点
是抛物线上的点,过点![]() 作
作![]() 轴的垂线与直线
轴的垂线与直线![]() 交于点
交于点![]() ,求证:
,求证:![]() ;
;
(3)当![]() 时等边三角形时,求
时等边三角形时,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一台实物投影仪,图2是它的示意图,折线O﹣A﹣B﹣C表示支架,支架的一部分O﹣A﹣B是固定的,另一部分BC是可旋转的,线段CD表示投影探头,OM表示水平桌面,AO⊥OM,垂足为点O,且AO=7cm,∠BAO=160°,BC∥OM,CD=8cm.
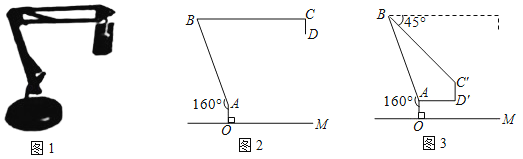
将图2中的BC绕点B向下旋转45°,使得BCD落在BC′D′的位置(如图3所示),此时C′D′⊥OM,AD′∥OM,AD′=16cm,求点B到水平桌面OM的距离,(参考数据:sin70°≈0.94,cos70°≈0.34,cot70°≈0.36,结果精确到1cm)
查看答案和解析>>
科目:初中数学 来源: 题型:
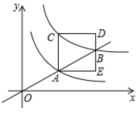
【题目】如图,过原点的直线与反比例函数y=![]() (x>0)、反比例函数y=
(x>0)、反比例函数y=![]() (x>0)的图象分别交于A、B两点,过点A作y轴的平行线交反比例函数y=
(x>0)的图象分别交于A、B两点,过点A作y轴的平行线交反比例函数y=![]() (x>0)的图象于C点,以AC为边在直线AC的右侧作正方形ACDE,点B恰好在边DE上,则正方形ACDE的面积为______.
(x>0)的图象于C点,以AC为边在直线AC的右侧作正方形ACDE,点B恰好在边DE上,则正方形ACDE的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图象是直线
的图象是直线![]() ,点A(14,1)是
,点A(14,1)是![]() 与反比例函数y=
与反比例函数y=![]() 的图象的交点.
的图象的交点.
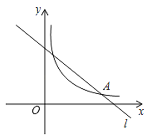
(1)一次函数与反比例函数的表达式;
(2)将直线![]() 平移后得直线
平移后得直线![]() ,与y轴正半轴交于点B(0,t),同时交
,与y轴正半轴交于点B(0,t),同时交![]() 轴于点C,若S△ABC=18,求t的值.
轴于点C,若S△ABC=18,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于点G,下列结论:①![]() ;②AG=
;②AG=![]() GC;③BE+DF=EF;④
GC;③BE+DF=EF;④![]() .其中正确的是( )
.其中正确的是( )

A.①②③B.①③④C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程大位是我国明朝商人,珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法.书中有如下问题:
一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚得几丁.
意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,下列求解结果正确的是( )

A. 大和尚25人,小和尚75人 B. 大和尚75人,小和尚25人
C. 大和尚50人,小和尚50人 D. 大、小和尚各100人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中
中![]() 是直径,点
是直径,点![]() 是
是![]() 上一点,点
上一点,点![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 的切线,与
的切线,与![]() 、
、![]() 的延长线分别交于点
的延长线分别交于点![]() 、
、![]() ,连接
,连接![]() .
.
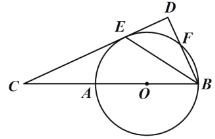
(1)求证:![]() .
.
(2)已知![]() 的半径为2,当
的半径为2,当![]() 为何值时,
为何值时,![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,M,N分别为锐角∠AOB的边OA,OB上的点,ON=6,把△OMN沿MN折叠,点O落在点C处,MC与OB交于点P,若MN=MP=5,则PN=( )
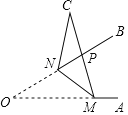
A.2B.3C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com