
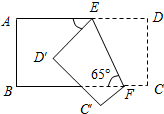
 如图,把一张长方形纸片沿EF折叠后,点D、C分别落在D′,C′的位置,若∠EFB=65°,求∠AED′和∠BFC′的度数.
如图,把一张长方形纸片沿EF折叠后,点D、C分别落在D′,C′的位置,若∠EFB=65°,求∠AED′和∠BFC′的度数. 分析 先根据平行线的性质得出∠EFB=∠DEF,再由图形翻折变换的性质得出∠DEF=∠D′EF,根据平角的定义可得出∠AED′的度数;同理,由平角的定义得出∠EFC的度数,根据图形翻折变换的性质得出∠CFE=∠BFE,再由∠EFB=65°即可得出结论.
解答 解:∵AD∥BC,∠EFB=65°,
∴∠EFB=∠DEF=65°,
∵四边形ED′C′F由四边形EDCF翻折而成,
∴∠DEF=∠D′EF=65°,
∴∠AED′=180°-65°-65°=50°.
∵∠EFB=65°,
∴∠EFC=180°-65°=115°.
∵四边形ED′C′F由四边形EDCF翻折而成,
∴∠CFE=∠BFE,
∴∠BFC′=115-65°=50°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:选择题
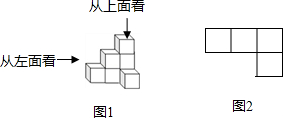 我们从不同的方向观察同一个物体时,可以看到不同的平面图,图1是由若干个小正方体所搭成的立体图形,图2是从图1的上面看这个立体图形时所看到的平面图,那么从图1的左面看这个立体图形,所看到的平面图是( )
我们从不同的方向观察同一个物体时,可以看到不同的平面图,图1是由若干个小正方体所搭成的立体图形,图2是从图1的上面看这个立体图形时所看到的平面图,那么从图1的左面看这个立体图形,所看到的平面图是( )| A. | 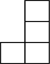 | B. |  | C. | 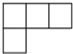 | D. | 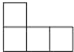 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
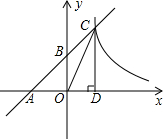 如图,已知一次函数y=kx+b(k≠0)的图象分别与x轴、y轴相交于A、B两点,并且与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于第一象限内的一点C,线段CD⊥x轴于点D,OA=OB=OD=1.
如图,已知一次函数y=kx+b(k≠0)的图象分别与x轴、y轴相交于A、B两点,并且与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于第一象限内的一点C,线段CD⊥x轴于点D,OA=OB=OD=1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
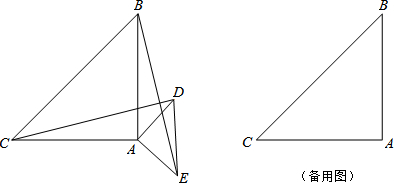
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
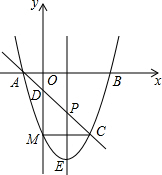 抛物线y=x2+bx+c与x轴交于点A(-1,0),B(3,0)两点,过点A的直线交抛物线于点C(2,m),交y轴于点D.
抛物线y=x2+bx+c与x轴交于点A(-1,0),B(3,0)两点,过点A的直线交抛物线于点C(2,m),交y轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45°,且AE+AF=2$\sqrt{3}$,则平行四边形的周长4$\sqrt{6}$.
如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45°,且AE+AF=2$\sqrt{3}$,则平行四边形的周长4$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 150° | B. | 120° | C. | 90° | D. | 60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com