
【题目】已知:如图1,点![]() 、
、![]() 、
、![]() 依次在直线
依次在直线![]() 上,现将射线
上,现将射线![]() 绕点
绕点![]() 沿顺时针方向以每秒
沿顺时针方向以每秒![]() 的速度旋转,同时射线
的速度旋转,同时射线![]() 绕点
绕点![]() 沿逆时针方向以每秒
沿逆时针方向以每秒![]() 的速度旋转,如图
的速度旋转,如图![]() ,设旋转时间为
,设旋转时间为![]() (
(![]() 秒
秒![]() 秒).
秒).
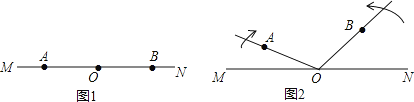
(1)用含![]() 的代数式表示
的代数式表示![]() 的度数.
的度数.
(2)在运动过程中,当![]() 第二次达到
第二次达到![]() 时,求
时,求![]() 的值.
的值.
(3)在旋转过程中是否存在这样的![]() ,使得射线
,使得射线![]() 是由射线
是由射线![]() 、射线
、射线![]() 、射线
、射线![]() 中的其中两条组成的角(指大于
中的其中两条组成的角(指大于![]() 而不超过
而不超过![]() 的角)的平分线?如果存在,请直接写出
的角)的平分线?如果存在,请直接写出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
【答案】(1)∠MOA=2t;(2)40秒;(3)t的值分别为18、22.5、36、67.5秒.
【解析】
(1)∠AOM的度数等于OA旋转速度乘以旋转时间;
(2)当∠AOB第二次达到60°时,射线OB在OA的左侧,根据∠AOM+∠BON-∠MON=60°列方程求解可得;
(3)射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角的平分线有三种情况:
①OB平分∠AOM时,根据![]() ∠AOM=∠BOM,列方程求解,
∠AOM=∠BOM,列方程求解,
②OB平分∠MON时,根据∠BOM=![]() ∠MON,列方程求解,
∠MON,列方程求解,
③OB平分∠AON时,根据∠BON=![]() ∠AON,列方程求解.
∠AON,列方程求解.
(1)由题意得:∠MOA=2t;
(2)如图,

根据题意知:∠AOM=2t,∠BON=4t,
当∠AOB第二次达到60°时,∠AOM+∠BON-∠MON=60°,
即2t+4t-180=60,解得:t=40,
故t=40秒时,∠AOB第二次达到60°;
(3)射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角的平分线有以下三种情况:
①OB平分∠AOM时,
∵![]() ∠AOM=∠BOM,
∠AOM=∠BOM,
∴t=180-4t,
解得:t=36;
②OB平分∠MON时,
∵∠BOM=![]() ∠MON,即∠BOM=90°,
∠MON,即∠BOM=90°,
∴4t=90,或4t-180=90,
解得:t=22.5,或t=67.5;
③OB平分∠AON时,
∵∠BON=![]() ∠AON,
∠AON,
∴4t=![]() (180-2t),
(180-2t),
解得:t=18;
综上,当t的值分别为18、22.5、36、67.5秒时,射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角的平分线.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案科目:初中数学 来源: 题型:
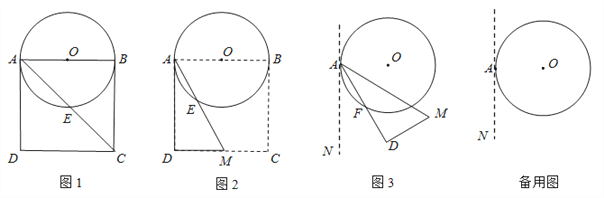
【题目】如图1,以边长为8的正方形纸片ABCD的边AB为直径作⊙O,交对角线AC于点E.
(1)线段AE=____________;
(2)如图2,以点A为端点作∠DAM=30°,交CD于点M,沿AM将四边形ABCM剪掉,使Rt△ADM绕点A逆时针旋转(如图3),设旋转角为α(0°<α<150°),旋转过程中AD与⊙O交于点F.
①当α=30°时,请求出线段AF的长;
②当α=60°时,求出线段AF的长;判断此时DM与⊙O的位置关系,并说明理由;
③当α=___________°时,DM与⊙O相切。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的文字,然后按要求解题:
例:1+2+3+ … +100=?
如果一个一个顺次相加显然太繁琐,我们仔细分析这100个连续自然数的规律和特点,可以发现运用加法运算律,是可以大大简化计算,提高运算速度的.
因为1+100=2+99=3+98= … =50+51=101
所以将所给算式中各加数经过交换、结合以后,可以很快求出结果.
解:1+2+3+ … +100
=(1+100)+(2+99)+(3+98)+ … +(50+51)
=101×____________
=____________ .
(1)补全例题的解题过程;
(2)计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,用棋子摆成的“上”字:

第一个“上”字 第二个“上”字 第三个“上”字
如果按照以上规律继续摆下去,那么通过观察,可以发现:
(1)第四、第五个“上”字分别需用 和 枚棋子.
(2)第n个“上”字需用 枚棋子.
(3)如果某一图形共有102枚棋子,你知道它是第几个“上”字吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子).下列叙述正确的是( )

A. 赛跑中,兔子共休息了50分钟
B. 乌龟在这次比赛中的平均速度是0.1米/分钟
C. 兔子比乌龟早到达终点10分钟
D. 乌龟追上兔子用了20分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形AECF中,![]() .CE、CF分别是△ABC的内,外角平分线.
.CE、CF分别是△ABC的内,外角平分线.

(1)求证:四边形AECF是矩形.
(2)当△ABC满足什么条件时,四边形AECF是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
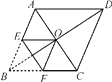
【题目】如图,菱形ABCD的对角线相交于点O,AC=2,BD=2![]() ,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________
,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________
查看答案和解析>>
科目:初中数学 来源: 题型:
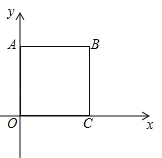
【题目】如图,正方形OABC∽正方形ODEF,它们是以原点O为位似中心的位似图形,位似比为1: ![]() , 点A的坐标为(0,1),则点E的坐标是________或________.
, 点A的坐标为(0,1),则点E的坐标是________或________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
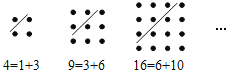
A.13=3+10B.25=9+16C.36=15+21D.49=18+31
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com