
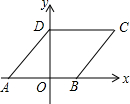
 如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A、B的坐标分别为(-3,0)、(2,0),且点D在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k的值为20.
如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A、B的坐标分别为(-3,0)、(2,0),且点D在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k的值为20. 科目:初中数学 来源: 题型:选择题
| A. | x2-x=2 | B. | x+5y=3 | C. | $\frac{1}{x}$+1=$\frac{x}{2}$ | D. | $\frac{1}{2}$+x=$\frac{x}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
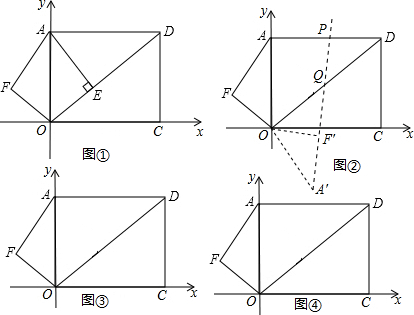
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
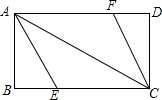 同学张丰用一张长18cm、宽12cm矩形纸片折出一个菱形,他沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到四边形AECF(如图).
同学张丰用一张长18cm、宽12cm矩形纸片折出一个菱形,他沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到四边形AECF(如图).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
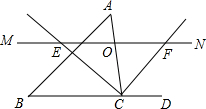 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 老北京的老行当中有一行叫做“抓彩卖糖”:商贩将高丽纸裁成许多小条,用矾水在上面写上糖的块数,最少一块,多的是三块或五块,再将枝条混合在一起.游戏时叫儿童随意抽取一张,然后放入水罐中浸湿,即出现白道儿,按照上面的白道儿数给糖.一个商贩准备了10张质地均匀的纸条,其中能得到一块糖的纸条有5张,能得到三块塘的纸条有3张,能得到五块糖的纸条有2张.从中随机抽取一张纸条,恰好是能得到三块塘的纸条的概率是( )
老北京的老行当中有一行叫做“抓彩卖糖”:商贩将高丽纸裁成许多小条,用矾水在上面写上糖的块数,最少一块,多的是三块或五块,再将枝条混合在一起.游戏时叫儿童随意抽取一张,然后放入水罐中浸湿,即出现白道儿,按照上面的白道儿数给糖.一个商贩准备了10张质地均匀的纸条,其中能得到一块糖的纸条有5张,能得到三块塘的纸条有3张,能得到五块糖的纸条有2张.从中随机抽取一张纸条,恰好是能得到三块塘的纸条的概率是( )| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com