
 萧山地铁2号线的开通使银隆百货车流量增大,为方便消费者停车,拟将商场门口某区域边界处有台阶五级,每个台阶高150mm,宽300mm,现把台阶处改建为斜坡以方便汽车出入.为保证不损坏车的底盘,台阶下面设置缓坡带,使斜坡角为5.711°,则台阶下面增加缓坡带的水平宽OA为多少m?(参考tan5.711°≈0.1000,sin5.711°≈0.09951.,cos5.711°≈0.9950)
萧山地铁2号线的开通使银隆百货车流量增大,为方便消费者停车,拟将商场门口某区域边界处有台阶五级,每个台阶高150mm,宽300mm,现把台阶处改建为斜坡以方便汽车出入.为保证不损坏车的底盘,台阶下面设置缓坡带,使斜坡角为5.711°,则台阶下面增加缓坡带的水平宽OA为多少m?(参考tan5.711°≈0.1000,sin5.711°≈0.09951.,cos5.711°≈0.9950) 科目:初中数学 来源: 题型:解答题
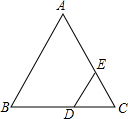 已知:如图,△ABC中,AB=AC,D为BC上一点,过点D作DE∥AB交AC于点E.
已知:如图,△ABC中,AB=AC,D为BC上一点,过点D作DE∥AB交AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 定义:如果三角形有一边上的中线长恰好等于这边的长,那么称该三角形为“特别三角形”.
定义:如果三角形有一边上的中线长恰好等于这边的长,那么称该三角形为“特别三角形”.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
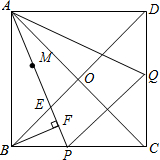
 如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )
如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )| A. | 115° | B. | 105° | C. | 95° | D. | 85° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
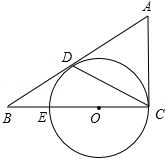 如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 448×108 | B. | 44.8×109 | C. | 4.48×1010 | D. | 4×1010 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com