Question

15．定义：如果三角形有一边上的中线长恰好等于这边的长，那么称该三角形为“特别三角形”．
如图，在正方形ABCD中，对角线AC，BD交于点O，P为BC边上的任意一点（不与B，C重合），DC边上的点Q与P点关于AC对称，AP与BD交于点E，BF⊥AP于点F．
（1）给定条件：①AP平分∠BAC，②BP：AB=$\sqrt{3}$：2；结论：①Rt△ABP为“特别三角形”，②AE=2BF．请从中各选一个条件和结论，组成两个正确的命题，并证明其中一个命题；
（2）设BP=m，PC=n，若△APQ是“特别三角形”，试求$\frac{m}{n}$的值；
（3）若正方形ABCD的边长为4cm，一动点M从A点出发，沿线段AP，PC运动至C点停止，在线段AP上的速度为1cm/s，在线段PC上的速度为2cm/s，则点M在整个运动过程中最少用时多少秒？

Answer 1

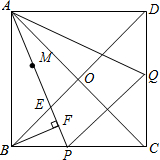
分析 （1）如图1，延长BF交AC于点G，易证△AOE≌△BOG，BG=AE，易证△ABG为等腰三角形，由于AP平分∠BAC，所以AE=BG=2BF；
（2）如图2，设AC与PQ交于点N，正方形边长为a，延长AB交QP的延长线于点K，由于点Q，P关于直线AC对称，得到PC=CQ，∠ACP=∠ACQ=45°，∠ANK=∠CNP=90°，AP=AQ，PN=QN，所以∠CAB=∠ACP，∠K=45°△ANK∽△CNP．BK=BP=m，于是得到结论$\frac{AN}{CN}=\frac{AK}{CP}=\frac{AB+BK}{CP}=\frac{a+m}{n}=\frac{2m+n}{n}$；
（3）设运动时间为t，则t=AP+$\frac{1}{2}$PC，如图4，取∠BCN’=30°，交AB延长线于点N′，作PG′⊥N′C，于是得到$\frac{1}{2}$PC=PN′，t=AP+PG′，当A，P，G′在一直线，即AP⊥NC时t最小，如图AH′⊥N′C，交BC于P′，点P在点P′位置时t最小，由∠BCN′=30°得BN′=$\frac{{4\sqrt{3}}}{3}$由∠N′=60°，得到最小t=AH′=$2（\sqrt{3}+1）$，得到结论：运动一周的最少用时为 $2（\sqrt{3}+1）$秒．

解答 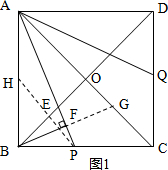解（1）命题1：若AP平分∠BAC，则AE=2BF，
命题2：若BP：AB=$\sqrt{3}$：2，则Rt△ABP为“特别三角形”，
证明：如图1，延长BF交AC于点G，
在正方形ABCD中，对角线AC，BD交于点O，
∴AO=BO，∠AOB=∠BOC，
∵∠OAE+∠AEO=∠EBF+∠BEF=90°，∠AEO=∠BEO
∴∠EAO=∠EBF，
在△AOB与△BOC中，
$\left\{\begin{array}{l}{∠AOB=∠BOC}\\{AO=BO}\\{∠AEO=∠BEO}\end{array}\right.$，
∴△AOE≌△BOG（ASA），
∴BG=AE，
∵AP平分∠BAC，
∴∠BAP=∠CAP，
∵∠BAP=∠BAC-∠PAC，∠CBG=∠CBO-∠GBO，
∴∠BAP=∠OBG，
∴∠ABO+∠OBG=∠ACB+∠GBC，
∴∠ABG=∠AGB，
∴AB=AG
∵AP平分∠BAC，
∴AE=BG=2BF，
证明2：取AB中点H，连接PH．
∵BP：AB=$\sqrt{3}$：2，
设AB=2x，BP=$\sqrt{3}$x，
∵∠ABP=90°，BH=x，
∴PH=2x，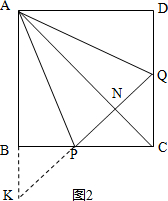
∴PH=AB，
∴Rt△ABP为“特别三角形”；

（2）如图2，设AC与PQ交于点N，正方形边长为a，
延长AB交QP的延长线于点K，
∵点Q，P关于直线AC对称，
∴PC=CQ，∠ACP=∠ACQ=45°，∠ANK=∠CNP=90°，
AP=AQ，PN=QN，
∴∠CAB=∠ACP，∠K=45°，
∴△ANK∽△CNP，BK=BP=m，
∴$\frac{AN}{CN}=\frac{AK}{CP}=\frac{AB+BK}{CP}=\frac{a+m}{n}=\frac{2m+n}{n}$，
①当等腰△APQ中底边PQ与它的中线AN相等，即AN=PQ时，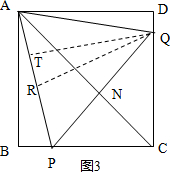
PN=CN=$\frac{1}{2}$AN$\frac{AN}{CN}=\frac{2m+n}{n}=2$，∴$\frac{m}{n}=\frac{1}{2}$，
②如图3当等腰△APQ中腰AP与它的中线QR相等，即AP=QR=AQ时，
作QT⊥AP于T，
∴RT=AT=$\frac{1}{2}$AR=$\frac{1}{4}$AP，
设RT=x，
∴AQ=AP=4x，
∴QT=$\sqrt{15}$x，PQ=$2\sqrt{6}$x，
∴PN=CN=$\sqrt{6}$x，
∵AP•QT=PQ•AN，
∴AN=$\sqrt{10}$x，
∴$\frac{AN}{CN}=\frac{2m+n}{n}$=$\frac{{\sqrt{15}}}{3}$，
∴$\frac{m}{n}=\frac{{\sqrt{15}-3}}{6}$；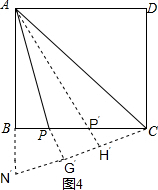

（3）设运动时间为t，则t=AP+$\frac{1}{2}$PC
如图4，取∠BCN′=30°，交AB延长线于点N′，作PG′⊥N′C，
∴$\frac{1}{2}$PC=PG′，
∴t=AP+PG′，
∴当A、P、G′在一直线，即AP⊥NC时t最小，
如图AH′⊥N′C交BC于P′，点P在点P′位置时t最小，
∴由∠BCN′=30°得BN′=$\frac{{4\sqrt{3}}}{3}$，由∠N′=60°得最小t=AH′=$2（\sqrt{3}+1）$，
∴运动一周的最少用时为 $2（\sqrt{3}+1）$秒．

点评 本题主要考查了最短路线问题，考查轴对称的性质的运用，全等三角形的判定及性质的运用，勾股定理的运用，相似三角形的判定及性质的运用，等边三角形的性质的运用等知识点．