
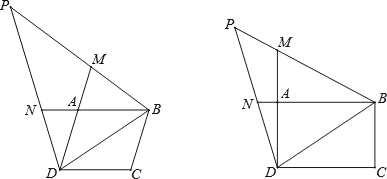
【题目】如图,在平行四边形ABCD中,点M、N分别在线段DA、BA的延长线上,且BD=BN=DM,连接BM、DN并延长交于点P.
(1)求证:∠P=90°﹣![]() ∠C;
∠C;
(2)当∠C=90°,ND=NP时,判断线段MP与AM的数量关系,并给予证明.
【答案】(1)证明见解析;(2)![]()
【解析】分析(1)首先过点B作BF⊥PD于点F,过点D作DG⊥BP于点G,BF与DG交于点H,由BD=BN=DM,可得BF与DG是∠DBN、∠MDB的平分线,又由四边形内角和为360°,可得∠P+∠FHG=180°,继而可得∠DHB=∠FHG=180°-∠P=90°+![]() ∠C,则可证得结论;
∠C,则可证得结论;
(2)首先过点P作PS⊥CD于点S,PR⊥BC于点R,易证得△PKD≌△PSD(AAS),同理:△PKB≌△PRB,然后延长BN交QS于点Q,则Q为PS的中点,设QS=PQ=x,即可求得答案.
详解(1)证明:过点B作BF⊥PD于点F,过点D作DG⊥BP于点G,BF与DG交于点H,
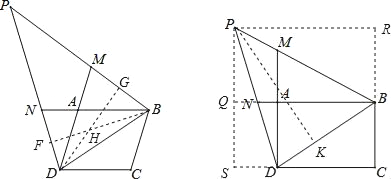
∴∠FHG+∠P=180°,
∴∠DHB+∠P=180°,
∴∠DHB=180°﹣∠P,
∵BD=BN=DM,
∴BF与DG是∠DBN、∠MDB的平分线,
∴由四边形内角和为360°,可得∠P+∠FHG=180°,
∵∠DHB=180°﹣(∠GDB+∠FBD)=180°﹣![]() (180°﹣∠DAB)=90°﹣
(180°﹣∠DAB)=90°﹣![]() ∠DAB,
∠DAB,
∵四边形ABCD是平行四边形,
∴∠DAB=∠C,
∴∠DHB=90°﹣![]() ∠C,
∠C,
∵∠DHB=180°﹣∠P,
∴180°﹣∠P=90°+![]() ∠C,
∠C,
∴∠P=90°﹣![]() ∠C;
∠C;
(2)MP:AM=![]() :2.
:2.
理由:过点P作PS⊥CD于点S,PR⊥BC于点R,
当∠C=90°时,则∠DPB=45°,
∵BN∥CD,
∴∠BND=∠BDN=∠SDN,
同理:∠PBD=∠PBR,
作PK⊥BD于点K,
在△PKD和△PSD中,
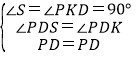
∴△PKD≌△PSD(AAS),
同理:△PKB≌△PRB,
∴PS=PR,
∴四边形PSCR是正方形,
延长BN交QS于点Q,则Q为PS的中点,
设QS=PQ=x,
则PS=CS=RC=2x,RB=KB=x,
设SD=m,BD=x+m,
则(x+m)2=x2+(2x﹣m)2,
∴m:x=2:3,
∴DK=SD=![]() x,BD=
x,BD=![]() x,
x,
∴AM=DM﹣AD=BD﹣AD=![]() x,
x,
根据勾股定理得,AB=![]() =
=![]() x,
x,
在Rt△ABM中,BM=![]() ,
,
∴PB=![]() ,
,
∴PM=![]() ,
,
∴MP:AM=![]() :2.
:2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板的两直角边所在直线分别与直线BC,CD交于点M,N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是__________________;
(2)如图2,若点O在正方形的中心(即两对角线的交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说理)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》卷九“勾股”中记载:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问霞长几何.
注释:今有正方形水池边长1丈,芦苇生长在中央,长出水面1尺.将芦苇向池岸牵引,恰好与水岸齐,问芦苇的长度(一丈等于10尺).解决下列问题:
(1)示意图中,线段![]() 的长为______尺,线段
的长为______尺,线段![]() 的长为______尺;
的长为______尺;

(2)求芦苇的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
(1)获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.
(1)如图1,当点E在边DC上自D向C移动,同时点F在边CB上自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的数量关系和位置关系,并说明理;
(2)如图2,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不需证明);连接AC,求△ACE为等腰三角形时CE:CD的值;
(3)如图3,当E,F分别在直线DC,CB上移动时,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP的最大值.
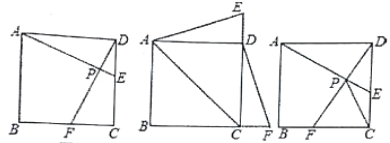
图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,曲线AB是顶点为B,与y轴交于点A的抛物线y=﹣x2+4x+2的一部分,曲线BC是双曲线y=![]() 的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2018,m)与Q(2025,n)均在该波浪线上,则
的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2018,m)与Q(2025,n)均在该波浪线上,则![]() =___________.
=___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB,反向延长线段AB到C,使BC=![]() AB,D为BC的中点,E为BD的中点.
AB,D为BC的中点,E为BD的中点.
(1)①补全图形;
②若AB=4,则AE=_____(直接写出结果).
(2)若AE=2,求AC的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是本地区一种产品30天的销售图象,图1是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图2是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )

A. 第24天的销售量为200件 B. 第10天销售一件产品的利润是15元
C. 第12天与第30天这两天的日销售利润相等 D. 第30天的日销售利润是750元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com