
【题目】已知线段AB,反向延长线段AB到C,使BC=![]() AB,D为BC的中点,E为BD的中点.
AB,D为BC的中点,E为BD的中点.
(1)①补全图形;
②若AB=4,则AE=_____(直接写出结果).
(2)若AE=2,求AC的长.
![]()
 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形OABC中,点A,C分别在x轴,y轴的正半轴上,OA=4,OC=2.点P(m,0)是射线OA上的动点,E为PC中点,作□OEAF,EF交OA于G,
(1)写出点E,F的坐标(用含m的代数式表示):E(_____,_____),F(______,_____).
(2)当线段EF取最小值时,m的值为______;此时□OEAF的周长为______.
(3)①当□OEAF是矩形时,求m的值.
②将△OEF沿EF翻折到△O′EF,若△O′EF与△AEF重叠部分的面积为1时,m的值为 .


查看答案和解析>>
科目:初中数学 来源: 题型:
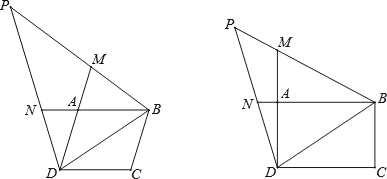
【题目】如图,在平行四边形ABCD中,点M、N分别在线段DA、BA的延长线上,且BD=BN=DM,连接BM、DN并延长交于点P.
(1)求证:∠P=90°﹣![]() ∠C;
∠C;
(2)当∠C=90°,ND=NP时,判断线段MP与AM的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是线段
是线段![]() 上任一点,
上任一点,![]() ,
,![]() 两点分别从
两点分别从![]() 同时向
同时向![]() 点运动,且
点运动,且![]() 点的运动速度为
点的运动速度为![]() ,
,![]() 点的运动速度为
点的运动速度为![]() ,运动的时间为
,运动的时间为![]() .
.
(1)若![]() ,
,
①运动![]() 后,求
后,求![]() 的长;
的长;
②当![]() 在线段
在线段![]() 上运动时,试说明
上运动时,试说明![]() ;
;
(2)如果![]() 时,
时,![]() ,试探索
,试探索![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
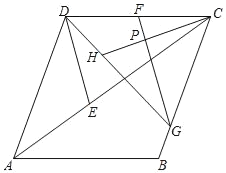
【题目】已知:如图,在□ABCD中,E、F分别为BC、AD的中点.
(1)试判断四边形AECF是什么四边形?为什么?
(2)当AB⊥AC时,四边形AECF是什么四边形?
(3)结合图形,请你添加一个条件,使其与原已知条件共同能推出四边形AECF是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在菱形ABCD中,AC是对角线,CD=CE,连接DE.
(1)若AC=16,CD=10,求DE的长.
(2)G是BC上一点,若GC=GF=CH且CH⊥GF,垂足为P,求证:![]() DH=CF.
DH=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
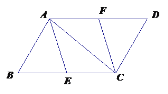
【题目】数学活动课上,励志学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
在证明这道题时,励志学习小组成员小颖同学进行如下书写,请你将此证明过程补充完整
证明:设DH=x,由由题意,CD=2x,CH=![]() x,
x,
∴AD=2AB=4x,
∴AH=AD﹣DH=3x,
∵CH⊥AD,
∴AC=![]() =2
=2![]() x,
x,
(3)深入探究
在(2)的条件下,励志学习小组成员小漫同学探究发现![]() ,试判断小漫同学的结论是否正确,并说明理由
,试判断小漫同学的结论是否正确,并说明理由

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与x轴交点A(1,0),B(-3,0) .与y轴交点B(0,3),如图1所示,D为抛物线的顶点。
与x轴交点A(1,0),B(-3,0) .与y轴交点B(0,3),如图1所示,D为抛物线的顶点。
(1)求抛物线的解析式;
(2)如图1若R为y轴上的一个动点,连接AR,则![]()
![]() RB+AR的最小值为
RB+AR的最小值为
(3)在x轴上取一动点P(m,0),![]() ,过点P作x轴的垂线,分别交抛物线、CD、CB于点Q、F、E,如图2所示,求证EF=EP.
,过点P作x轴的垂线,分别交抛物线、CD、CB于点Q、F、E,如图2所示,求证EF=EP.
(4)设此抛物线的对称轴为直线MN,在直线MN上取一点T,使∠BTN=∠CTN.直接写出点T的坐标。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com