
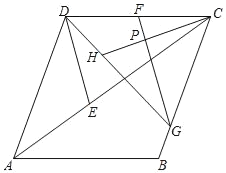
【题目】如图所示,在菱形ABCD中,AC是对角线,CD=CE,连接DE.
(1)若AC=16,CD=10,求DE的长.
(2)G是BC上一点,若GC=GF=CH且CH⊥GF,垂足为P,求证:![]() DH=CF.
DH=CF.
【答案】(1)2![]() (2)见解析
(2)见解析
【解析】
(1)连接BD交AC于K.想办法求出DK,EK,利用勾股定理即可解决问题;
(2)证明:过H作HQ⊥CD于Q,过G作GJ⊥CD于J.想办法证明∠CDH=∠HGJ=45°,可得DH=![]() QH解决问题.
QH解决问题.
(1)解:连接BD交AC于K.
∵四边形ABCD是菱形,
∴AC⊥BD,AK=CK=8,
在Rt△AKD中,DK=![]() =6,
=6,
∵CD=CE,
∴EK=CE﹣CK=10﹣8=2,
在Rt△DKE中,DE=![]() =2
=2![]() .
.
(2)证明:过H作HQ⊥CD于Q,过G作GJ⊥CD于J.
∵CH⊥GF,
∴∠GJF=∠CQH=∠GPC=90°,
∴∠QCH=∠JGF,
∵CH=GF,
∴△CQH≌△GJF(AAS),
∴QH=CJ,
∵GC=GF,
∴∠QCH=∠JGF=∠CGJ,CJ=FJ=![]() CF,
CF,
∵GC=CH,
∴∠CHG=∠CGH,
∴∠CDH+∠QCH=∠HGJ+∠CGJ,
∴∠CDH=∠HGJ,
∵∠GJF=∠CQH=∠GPC=90°,
∴∠CDH=∠HGJ=45°,
∴DH=![]() QH,
QH,
∴![]() DH=2QH=CF.
DH=2QH=CF.


科目:初中数学 来源: 题型:
【题目】《九章算术》卷九“勾股”中记载:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问霞长几何.
注释:今有正方形水池边长1丈,芦苇生长在中央,长出水面1尺.将芦苇向池岸牵引,恰好与水岸齐,问芦苇的长度(一丈等于10尺).解决下列问题:
(1)示意图中,线段![]() 的长为______尺,线段
的长为______尺,线段![]() 的长为______尺;
的长为______尺;

(2)求芦苇的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,曲线AB是顶点为B,与y轴交于点A的抛物线y=﹣x2+4x+2的一部分,曲线BC是双曲线y=![]() 的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2018,m)与Q(2025,n)均在该波浪线上,则
的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2018,m)与Q(2025,n)均在该波浪线上,则![]() =___________.
=___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB,反向延长线段AB到C,使BC=![]() AB,D为BC的中点,E为BD的中点.
AB,D为BC的中点,E为BD的中点.
(1)①补全图形;
②若AB=4,则AE=_____(直接写出结果).
(2)若AE=2,求AC的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
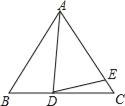
【题目】已知△ABC,AB=AC,D为BC上一点,E为AC上一点,AD=AE.
(1)如果∠BAD=10°,∠DAE=30°,那么∠EDC= °.
(2)如果∠ABC=60°,∠ADE=70°,那么∠BAD= °,∠CDE= °.
(3)设∠BAD=α,∠CDE=β猜想α,β之间的关系式,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
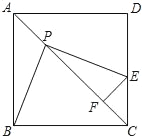
【题目】已知边长为1的正方形ABCD中, P是对角线AC上的一个动点(与点A、C不重合),过点P作PE⊥PB ,PE交射线DC于点E,过点E作EF⊥AC,垂足为点F.
(1)当点E落在线段CD上时(如图),
①求证:PB=PE;
②在点P的运动过程中,PF的长度是否发生变化?若不变,试求出这个不变的值,若变化,试说明理由;
(2)当点E落在线段DC的延长线上时,在备用图上画出符合要求的大致图形,并判断上述(1)中的结论是否仍然成立(只需写出结论,不需要证明);
(3)在点P的运动过程中,△PEC能否为等腰三角形?如果能,试求出AP的长,如果不能,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是本地区一种产品30天的销售图象,图1是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图2是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )

A. 第24天的销售量为200件 B. 第10天销售一件产品的利润是15元
C. 第12天与第30天这两天的日销售利润相等 D. 第30天的日销售利润是750元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com