
【题目】商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为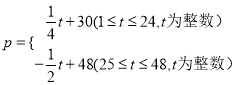 ,且其日销售量y(kg)与时间t(天)的关系如下表:
,且其日销售量y(kg)与时间t(天)的关系如下表:

(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
【答案】(1)y=-2t+120,当t=30时,y=60(kg)
(2)当t=10时,W最大=1250元
【解析】试题分析:(1)设y=kt+b,利用待定系数法即可解决问题.(2)日利润=日销售量×每公斤利润,据此分别表示前24天和后24天的日利润,根据函数性质求最大值后比较得结论.
试题解析:(1)设y=kt+b,把t=1,y=118;t=3,y=114代入得到:
![]() ,解得
,解得![]() ,
,
∴y=2t+120.
将t=30代入上式,得:y=2×30+120=60.
所以在第30天的日销售量是60kg.
(2)设第x天的销售利润为w元。
当1t24时,由题意w=(2t+120)( ![]() t+3020)=
t+3020)= ![]() (t10)2+1250,
(t10)2+1250,
∴t=10时w最大值为1250元。
当25t48时,w=(2t+120)(( ![]() t+4820)=t2116t+3360,
t+4820)=t2116t+3360,
∵对称轴t=58,a=1>0,
∴在对称轴左侧w随x增大而减小,
∴t=25时,w最大值=1085,
综上所述第10天利润最大,最大利润为1250元。


科目:初中数学 来源: 题型:
【题目】某校对九年级6个班学生平均一周的课外阅读时间进行了统计,分别为(单位:h):3.5,4,3.5,5,5,3.5.这组数据的众数是( )
A. 3 B. 3.5 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
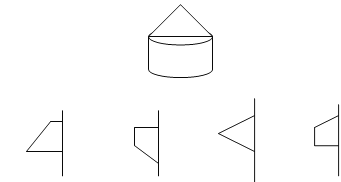
【题目】如图是一个粮仓,已知粮仓底面直径为8m,粮仓顶部顶点到地面的垂直距离为9m,粮仓下半部分高为6m,观察并回答下列问题:
(1)粮仓是由两个几何体组成的,他们分别是________;
(2)用一个平面去截粮仓,截面可能是____________(写出一个即可);
(3)如图,将下面的图形分别绕虚线旋转一周,哪一个能形成粮仓?用线连一连;
(4)求出该粮仓的容积(结果精确到0.1, ![]() 取3.14).
取3.14).
查看答案和解析>>
科目:初中数学 来源: 题型:
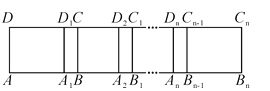
【题目】如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位长度,得到长方形A1B1C1D1,第2次平移长方形A1B1C1D1沿A1B1的方向向右平移5个单位长度,得到长方形A2B2C2D2,…,第n次平移长方形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向向右平移5个单位长度,得到长方形AnBnCnDn(n>2),若ABn的长度为2 016,则n的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,且AB =6,C是⊙O上一点,D是![]() 的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.
的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.
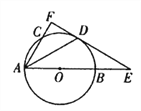
(l)求证:AF⊥EF;
(2)填空:
①当BE= 时,点C是AF的中点;
②当BE= 时,四边形OBDC是菱形,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三角形三边之长能求出三角形的面积吗?
海伦公式告诉你计算的方法是:S= ![]() ,其中S表示三角形的面积,a,b,c分别表示三边之长,p表示周长之半,即p=
,其中S表示三角形的面积,a,b,c分别表示三边之长,p表示周长之半,即p= ![]() .
.
我国宋代数学家秦九韶提出的“三斜求积术”与这个公式基本一致,所有这个公式也叫“海伦﹣秦九韶公式”.
请你利用公式解答下列问题.
(1)在△ABC中,已知AB=5,BC=6,CA=7,求△ABC的面积;
(2)计算(1)中△ABC的BC边上的高.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com