
���� ͨ�������A�����жϣ����ݷ��������������ʶԣ�2�������жϣ��Ȱ����ݰ���С�������У�Ȼ�������λ���������Ķ���ԣ�3�������жϣ����ݶ��θ�ʽ�����ʶԣ�4�������жϣ���Բ����Բ�İ뾶Ϊrcm������Բ��չ��ͼΪ���κͻ�����ʽ���r��Ȼ��ԣ�5�������жϣ�
��� �⣺x=2ʱ��x-2=0�����Է���$\frac{2}{x-2}+\frac{x}{2-x}$=0�⣬���ԣ�1������
����y=$\frac{4}{x}$����ÿһ���ޣ�y����x���������С�����ԣ�2������
���ݣ�3��5��4��2��3��6��4��3����С��������Ϊ��2��3��3��3��4��4��5��6�������������ݵ�������3����λ����3.5�����ԣ�3����ȷ��
��$\sqrt{{{��x-2��}^2}}$=x-2����x-2��0����x��2�����ԣ�4������
��Բ����Բ�İ뾶Ϊrcm����2��r=$\frac{150•��•12}{180}$�����r=5��cm�������ԣ�5����ȷ��
�ʴ�Ϊ��3����5����
���� ���⿼���������붨�����ж�һ���������䣬�������⣮�������ⶼ��������ͽ�����������ɣ���������֪�������������֪�����Ƴ������һ���������д�ɡ��������ô������ʽ�� ��Щ�������ȷ����������֤ʵ�ģ����������������������


 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������A1B1C1O��A2B2C2C1��A3B3C3C2��������ͼ��ʾ�ķ�ʽ����ƽ��ֱ������ϵ�У�
������A1B1C1O��A2B2C2C1��A3B3C3C2��������ͼ��ʾ�ķ�ʽ����ƽ��ֱ������ϵ�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
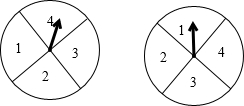 ��ͼ������ת�̷ֱ�����ת��һ�Σ���ת��ֹͣת��ʱ������ָ��ֱ�����ij����������ʾ�����������������ĺ������ĺ͵��ڣ�������
��ͼ������ת�̷ֱ�����ת��һ�Σ���ת��ֹͣת��ʱ������ָ��ֱ�����ij����������ʾ�����������������ĺ������ĺ͵��ڣ�������| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������������ͼ��ʾ�Ĺ���������ȥ����������ʵ���ԣ�n��m����ʾ��n�ţ������ҵ�m�������磨4��3����ʾʵ��9����192��ʾ������ʵ�����ǣ�20��2����
������������ͼ��ʾ�Ĺ���������ȥ����������ʵ���ԣ�n��m����ʾ��n�ţ������ҵ�m�������磨4��3����ʾʵ��9����192��ʾ������ʵ�����ǣ�20��2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com