
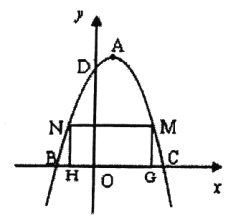
����Ŀ����ͼ����֪���κ���ͼ��Ķ�������Ϊ![]() ���������ύ��
���������ύ��![]() ��
��![]() ��
��![]() ���㣬��
���㣬��![]() �������Ϊ
�������Ϊ![]() .
.
��1������κ����Ľ���ʽ��
��2���ڶ��κ���ͼ��λ��![]() ���Ϸ���������������
���Ϸ���������������![]() ��
��![]() ���ҵ�
���ҵ�![]() �ڵ�
�ڵ�![]() ����࣬��
����࣬��![]() ��
��![]() ��
��![]() ��Ĵ��߽�
��Ĵ��߽�![]() ���ڵ�
���ڵ�![]() ��
��![]() ���㣬���ı���
���㣬���ı���![]() Ϊ����ʱ����þ����ܳ������ֵ��
Ϊ����ʱ����þ����ܳ������ֵ��
��3���ڣ�2���еľ����ܳ����ʱ������![]() ����֪��
����֪��![]() ��
��![]() ����һ���㣬����
����һ���㣬����![]() ��
��![]() �ᣬ��ֱ��
�ᣬ��ֱ��![]() �ڵ�
�ڵ�![]() ���Ƿ���������ĵ�
���Ƿ���������ĵ�![]() ��ʹֱ��
��ʹֱ��![]() ��
��![]() �ֳ����Ϊ
�ֳ����Ϊ![]() �������֣������ڣ�����õ�����ꣻ�������ڣ���˵������.
�������֣������ڣ�����õ�����ꣻ�������ڣ���˵������.
 ����ͼ
����ͼ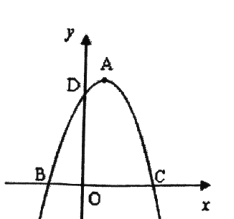
���𰸡���1��![]() ����2��20����3�����ڣ���
����2��20����3�����ڣ���![]() ������Ϊ
������Ϊ![]() ��
��![]()
��������
��1�����κ�������ʽΪ��![]() ������B�����������ʽ��������⣻
������B�����������ʽ��������⣻
��2�����![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ,
,![]() ������Ϊ
������Ϊ![]() ,�Ӷ����
,�Ӷ����![]() ;
;![]() �����Ծ���MNHG���ܳ�
�����Ծ���MNHG���ܳ�![]()
![]() ��������⣻
��������⣻
��3���������ܳ�ȡ�����ֵʱ��![]() ���Ӷ����
���Ӷ����![]() ��ֵ��Ȼ�����ֱ��
��ֵ��Ȼ�����ֱ��![]() �Ľ���ʽ�����
�Ľ���ʽ�����![]() ����Ϊ
����Ϊ![]() ������
������![]() �������
�������![]() �����
�����![]() ʱ����
ʱ����![]() �������
�������![]() �����
�����![]() ʱ��������ֱ��г����̣������P�����꣮
ʱ��������ֱ��г����̣������P�����꣮
�⣺��1������κ����Ľ���ʽΪ![]()
![]() ���κ���ͼ��Ķ�������Ϊ
���κ���ͼ��Ķ�������Ϊ![]()
![]()
![]()
��![]() ͼ����
ͼ����![]()
![]()
��ã�![]()
![]() ���κ����Ľ���ʽΪ
���κ����Ľ���ʽΪ![]()
��2��![]() �ı���
�ı���![]() Ϊ���Σ�
����
![]() ����ֱ��
����ֱ��![]() �Գ�
�Գ�
���![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]()
![]() ������Ϊ
������Ϊ![]()
![]() ;
;![]()
![]() ����
����![]() ���ܳ�
���ܳ�![]()
![]()
![]() ��
��![]() ʱ��
ʱ��
![]()
![]() �����ܳ������ֵΪ20.
�����ܳ������ֵΪ20.
��3�����ڣ��������£�
�������ܳ�ȡ�����ֵʱ��![]()
![]()
![]() ���Գ���Ϊֱ��
���Գ���Ϊֱ��![]()
![]()
![]()
��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]()
��![]() ������ʽ�ã�
������ʽ�ã�
![]() �����
�����![]()
![]()
���![]() ����Ϊ
����Ϊ![]()
![]()
�ٵ�![]() �������
�������![]() �����
�����![]() ʱ��
ʱ��
![]()
��ã�![]() ��
��![]() ����ȥ��
����ȥ��
![]()
�ڵ�![]() �������
�������![]() �����
�����![]() ʱ��
ʱ��
![]()
��ã�![]() ��
��![]() ����ȥ��
����ȥ��
![]()
������������![]() ������Ϊ
������Ϊ![]() ��
��![]()


 ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д�
ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ۺ���ֳ��������̬��ֳ����ɫ��չ��ij�����ۺ���ֳ���ƻ�����ף������ֺ̻������磬�����飬�õ�������Ϣ��
����������40 kg | ������������40 kg | |
������ | ԭ������ | ���������� |
������ | ԭ������ | ��������� |
�������10 kg�ļ������5 kg������������700Ԫ���������20 kg�ļ������15 kg������������1600Ԫ��
��1���������������ĵ��۸��Ƕ���Ԫ��
��2���־�������ף���������ƹ�90 kg�����У�����������������ڼ�����������2�����蹺�������a kg��![]() ���������ֳ����������������ܷ���W��a֮��ĺ�������ʽ��
���������ֳ����������������ܷ���W��a֮��ĺ�������ʽ��
��3���ڣ�2���������£������һ�ֹ�����ʹ�����ܷ�����ͣ����������ܷ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
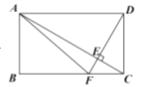
����Ŀ����ͼ���ھ���![]() �У�
��![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ���ӳ�
���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ����
����![]() ���߶�
���߶�![]() �ij�Ϊ__________��
�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
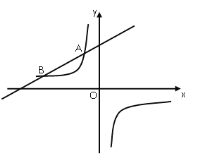
����Ŀ����ͼ��һ�κ���![]() ��
��![]() ��������
Ϊ��������![]() ����ͼ���뷴��������
����ͼ���뷴��������![]() ��ͼ����
��ͼ����![]() ��
��![]() ����.
����.
��1����һ�κ����ı���ʽ��
��2������ֱ��![]() ����ƽ��
����ƽ��![]() ����λ���Ⱥ��뷴����������ͼ������ֻ��һ�������㣬��
����λ���Ⱥ��뷴����������ͼ������ֻ��һ�������㣬��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������M��y��ax2+bx+c��a��0������A����1��0�����Ҷ�������ΪB��0��1����
��1����������M�ĺ�������ʽ��
��2����F��t��0��Ϊx����������һ�㣬��������M�Ƶ�F��ת180��õ�������M1��
��������M1�Ķ���B1������Ϊ�� ����
����������M1���߶�AB�й�����ʱ����Ϻ�����ͼ����t��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���´��ѽڣ����ӱ������䰲ȫ������Ⱦ��ʼ���Σ�ij�̵꾭��һ�ֵ��ӱ��ڣ���֪���ֵ��ӱ��ڵijɱ���Ϊÿ��80Ԫ���г����鷢�֣����ֵ��ӱ���ÿ���������y���У������۵���x��Ԫ�������¹�ϵ��y=��2x+320��80��x��160���������ֵ��ӱ���ÿ�����������ΪwԪ��
��1����w��x֮��ĺ�����ϵʽ��
��2�����ֵ��ӱ������۵��۶�Ϊ����Ԫʱ��ÿ����������������������Ƕ���Ԫ��
��3�����̵��������ֵ��ӱ���Ҫ��ÿ����2400Ԫ����������������ÿ죮��ô���۵���Ӧ��Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����ij�ֿ�ʽͯװ��һ����۳�30�ף�ÿ��ӯ��40Ԫ.Ϊ���������ۣ�����ӯ�����̳�������ȡ���۴�ʩ.��һ��ͯװÿ����1Ԫ��ƽ��ÿ��ɶ��۳�2�ף���ÿ��ͯװ����![]() Ԫʱ���̳�һ��ɻ�����
Ԫʱ���̳�һ��ɻ�����![]() Ԫ.
Ԫ.
��1����![]() ����
����![]() �ĺ�������ʽ.
�ĺ�������ʽ.
��2����Ҫ�̳�ÿ��ӯ��1500Ԫ����Ӧ���۶���Ԫ��
��3����ÿ��ͯװ���۶���Ԫʱ���̳��ɻ���������������Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�Ǿ��Σ��Ѿ�����AC�۵�����B���ڵ�E����AE��DC�Ľ���ΪO������DE��
��1����֤����ADE�ա�CED��
��2����֤��DE��AC��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com