
【题目】给出定义如下:若一对实数![]() 满足
满足![]() ,则称它们为 一对“相关数”,如:
,则称它们为 一对“相关数”,如:![]() ,故
,故![]() 是一对“相关数”.
是一对“相关数”.
(1)数对![]() 中是“相关数”的是___________;
中是“相关数”的是___________;
(2)若数对![]() 是“相关数”,求
是“相关数”,求![]() 的值;
的值;
(3)是否存在有理数数![]() ,使数对
,使数对![]() 和
和![]() 都是“相关数”,若存在,求出一对
都是“相关数”,若存在,求出一对![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)不存在,证明详见解析.
;(3)不存在,证明详见解析.
【解析】
(1)根据“相关数”的定义和公式进行计算,左右相等的即为答案;(2)代入新定义公式得到方程,解方程即可解答;(3)先假设存在,分别代入新定义公式,假设相等得:![]() ,只有0的相反数仍等于它本身等于0,所以得到
,只有0的相反数仍等于它本身等于0,所以得到![]() 的值不为
的值不为![]() ,即m-n≠mn+4,从而得解.
,即m-n≠mn+4,从而得解.
(1)∵数对(1,1):左边:a-b=1-1=0,右边:ab+4=1×1+4=5,左边≠右边,∴(1,1)不是;
数对(-2,-6):左边:a-b=-2-(-6)=4,右边:ab+4=(-2)×(-6)+4=16,左边≠右边,∴(-2,-6)不是;
数对(0,-4):左边:a-b=0-(-4)=4,右边:ab+4=0×(-4)+4=4,左边=右边,∴(0,-4)是;
即数对![]() 中是“相关数”的是
中是“相关数”的是![]() ;
;
(2)由题意得:![]()
解:![]()
![]()
![]()
![]()
答:![]()
(3)不存在.
理由:假设存在![]() 满足
满足![]() ,
,![]() 满足
满足![]() ,
,
且两个等式右边相同
![]()
![]() 若满足
若满足![]() ,则
,则![]() =
=![]()
![]() 的值不为
的值不为![]()
![]()
![]() 和
和![]() 的结果不同,
的结果不同,
![]()
![]()
综上所述,![]() 和
和![]() 的结果不同 ,不存在有理数
的结果不同 ,不存在有理数![]() ,使数对
,使数对![]() 和
和![]() 都是“相关数”,
都是“相关数”,


科目:初中数学 来源: 题型:
【题目】一些数学问题的研究可以经历观察、探究、发现、证明等过程.下面是对一个问题的部分研究过程:
(观察)![]() =
=![]() ,
,![]() =
=![]() ,
,![]() 是否也能写成分数的形式?
是否也能写成分数的形式?
(探究1)设![]() =x,
=x,
由![]() =0.555…可知,10x=5.555…,
=0.555…可知,10x=5.555…,
所以10x﹣x=5.
解方程,得x=![]()
于是,得![]() =
=![]() .
.
所以,![]() 能写成分数的形式
能写成分数的形式
(探究2)仿照上面的方法,尝试将![]() 写成分数的形式.
写成分数的形式.
(发现) .
请你完成(探究2)的部分,并用一句话概括你的发现
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△PBD∽△DCA;
(3)当AB=6,AC=8时,求线段PB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求1+2+22+23+24+25+26的值时,小明发现:从第二个加数起每一个加数都是前一个加数的2倍,于是他设:S=1+2+22+23+24+25+26①然后在①式的两边都乘以2,得:2S=2+22+23+24+25+26+27 ②;②﹣①得2S﹣S=27﹣1,S=27﹣1,即1+2+22+23+24+25+26=27﹣1.
(1)求1+3+32+33+34+35+36的值;
(2)求1+a+a2+a3+…+a2013(a≠0且a≠1)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
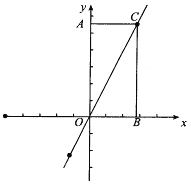
【题目】有一长方形AOBC纸片放在如图所示的坐标系中,且长方形的两边的比为OA:AC=2:1.
(1)求直线OC的解析式;
(2)求出![]() =-5时,函数
=-5时,函数![]() 的值;
的值;
(3)求出![]() =-5时,自变量
=-5时,自变量![]() 的值;
的值;
(4)画这个函数的图象;
(5)根据图象回答,当![]() 从2减小到-3时,
从2减小到-3时,![]() 的值是如何变化的?
的值是如何变化的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在线段上依次添加1个点,2个点,3个点,……,原线段上所成线段的总条数如下表:
添加点数 | 1 | 2 | 3 | 4 |
线段总条数 | 3 | 6 | 10 | 15 |
若在原线段上添加n个点,则原线段上所有线段总条数为( )
A. n+2 B. 1+2+3+…+n+n+1 C. n+1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)等于371元,请通过计算求出该商场购进甲、乙两种牛奶各自多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,BE平分∠ABC交CD边于点E.点F在BC边上,且FE⊥AE.
(1)如图1,①∠BEC=_________°;
②在图1已有的三角形中,找到一对全等的三角形,并证明你的结论;
(2)如图2,FH∥CD交AD于点H,交BE于点M.NH∥BE,NB∥HE,连接NE.若AB=4,AH=2,求NE的长.

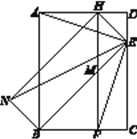
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=13,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=13,则: 若n=24,则第100次“F”运算的结果是________.
若n=24,则第100次“F”运算的结果是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com