
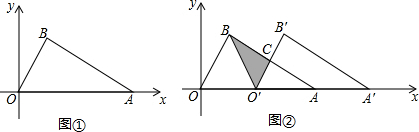
分析 (Ⅰ)由OB⊥AB,0A=4,OB=2得出△AOB是有一个角为30°的直角三角形,简单计算即可;
(Ⅱ)①由平移用m表示出BC,O′C,建立S=$\frac{\sqrt{3}}{8}$[-(m-2)2+4],即可;
②利用△BCO′为等腰三角形,则有CB=CO′确定出m,再利用相似求出CD,AD即可.
解答 解:(Ⅰ)∵OB⊥AB,0A=4,OB=2,
∴∠AOB=60°,∠OAB=30°,AB=2$\sqrt{3}$,
过点B作BD⊥OA,
∴OD=1,BD=$\sqrt{3}$,
∴B(1,$\sqrt{3}$).
(Ⅱ)①∵△A′O′B′是△OAB平移得到,
∴∠A′O′B′=∠AOB=60°,O′B′⊥AB,
∵OO′=m,
∴AO′=4-m,
∴O′C=$\frac{1}{2}$AO′=$\frac{1}{2}$(4-m),AC=$\frac{\sqrt{3}}{2}$AO′=$\frac{\sqrt{3}}{2}$(4-m),
∴BC=AB-AC=$\frac{\sqrt{3}}{2}$m,
∴S=$\frac{1}{2}$BC×O′C=$\frac{\sqrt{3}}{8}$m(4-m)=$\frac{\sqrt{3}}{8}$[-(m-2)2+4],
当m=2时,S最大=$\frac{\sqrt{3}}{2}$.
②如下图,作BE⊥OA,CD⊥OA,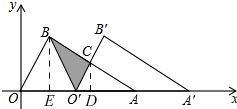
由①有,AO′=4-m,O′C=$\frac{1}{2}$(4-m),AC=$\frac{\sqrt{3}}{2}$(4-m),
∴CB=AB-AC=2$\sqrt{3}$-$\frac{\sqrt{3}}{2}$(4-m)=$\frac{\sqrt{3}}{2}$m,
由平移得,∠ACO′=∠ABO=90°,
∵△BCO′为等腰三角形,
∴CB=O′C,
∴$\frac{\sqrt{3}}{2}$m=$\frac{1}{2}$(4-m),
∴m=2($\sqrt{3}$-1).
∵BE×OA=OB×AB,
∴BE=$\frac{OB×AB}{OA}=\frac{2×2\sqrt{3}}{4}$=$\sqrt{3}$,
∴AE=$\sqrt{3}$BE=3,
∵△ACO′∽△ABO,
∴$\frac{CD}{BE}=\frac{AO′}{O′A′}$,
∴CD=$\frac{AO′}{O′A′}$×BE=$\frac{4-m}{4}$×$\sqrt{3}$=$\frac{4-2(\sqrt{3}-1)}{4}$×$\sqrt{3}$=$\frac{3\sqrt{3}-3}{2}$,
∵BE⊥OA,CD⊥OA,
∴BE∥CD,
∴$\frac{AD}{AE}=\frac{CD}{BE}$,
∴AD=$\frac{CD}{BE}$×AE=$\frac{3(3-\sqrt{3})}{2}$,
∴OD=OA-AD=4-$\frac{3(3-\sqrt{3})}{2}$=$\frac{3\sqrt{3}-1}{2}$,
∴C($\frac{3\sqrt{3}-1}{2}$,$\frac{3\sqrt{3}-3}{2}$).
点评 此题是几何变换综合题,考查了平移得性质,一个角为30°的直角三角形,相似三角形的判定和性质,用m表示出有关线段如(AO′=4-m,O′C=$\frac{1}{2}$(4-m),AC=$\frac{\sqrt{3}}{2}$(4-m),CB=$\frac{\sqrt{3}}{2}$m)是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
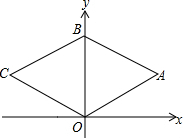 如图,菱形OABC顶点O是坐标原点,顶点B(0,6),OA=5.
如图,菱形OABC顶点O是坐标原点,顶点B(0,6),OA=5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$,1 | B. | -$\frac{1}{2}$,1 | C. | -$\frac{1}{2}$,-1 | D. | $\frac{1}{2}$,-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 400 | B. | 401 | C. | 402 | D. | 403 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
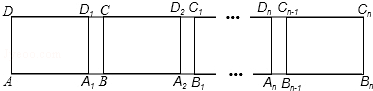
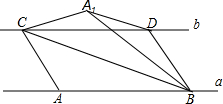 如图,直线a与b平行,点A、B是直线a上两个定点,点CD在直线b上运动(点C在点D的左侧),AB=CD=4cm,a、b之间的距离为$\sqrt{3}$cm,连接AC、BD、BC,把△ABC沿BC折叠得△A1BC.
如图,直线a与b平行,点A、B是直线a上两个定点,点CD在直线b上运动(点C在点D的左侧),AB=CD=4cm,a、b之间的距离为$\sqrt{3}$cm,连接AC、BD、BC,把△ABC沿BC折叠得△A1BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com