
ЁОЬтФПЁПвЛМвЪпВЫЙЋЫОМЦЛЎЕНФГТЬЩЋЪпВЫЛљЕиЪеЙКAЃЌBСНжжЪпВЫЙВ140ЖжЃЌдЄМЦСНжжЪпВЫЯњЪлКѓЛёРћЕФЧщПіШчЯТБэЫљЪОЃК
ЯњЪлЦЗжж | AжжЪпВЫ | BжжЪпВЫ |
УПЖжЛёРћ(дЊ) | 1200 | 1000 |
ЦфжаAжжЪпВЫЕФ5%ЃЌBжжЪпВЫЕФ3%аыдЫЭљCЪаГЁЯњЪлЃЌЕЋCЪаГЁЕФЯњЪлзмСПВЛГЌЙ§5.8ЖжЃЎЩшЯњЪлРћШѓЮЊWдЊ(ВЛМЦЫ№КФ)ЃЌЙКНјAжжЪпВЫxЖжЃЎ
ЃЈ1ЃЉЧѓWгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉНЋет140ЖжЪпВЫШЋВПЯњЪлЭъЃЌзюЖрПЩЛёЕУЖрЩйРћШѓЃП
ЃЈ3ЃЉгЩгкЪмЪаГЁвђЫигАЯьЃЌЙЋЫОНјЛѕЪБЕїВщЗЂЯжЃЌAжжЪпВЫУПЖжПЩЖрЛёРћ100дЊЃЌBжжЪпВЫУПЖжПЩЖрЛёРћm(200ЃМmЃМ400)дЊЃЌЕЋBжжЪпВЫЯњЪлЪ§СПВЛГЌЙ§90ЖжЃЎЙЋЫОЩшМЦСЫвЛжжЛёРћзюДѓЕФНјЛѕЗНАИЃЌЯњЪлЭъКѓПЩЛёРћ179000дЊЃЌЧѓmЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉWЃН200xЃЋ140000ЃЛЃЈ2ЃЉНЋет140ЖжЪпВЫШЋВПЯњЪлЭъЃЌзюЖрПЩЛёЕУРћШѓ156000дЊЃЛЃЈ3ЃЉ250
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЁАзмРћШѓ=ЯњЪлвЛЖжЪпВЫЕФРћШѓЁСЯњЪлСПЁБСаЪНМДПЩЃЛ
ЃЈ2ЃЉИљОнЁАAжжЪпВЫЕФ5%ЃЌBжжЪпВЫЕФ3%аыдЫЭљCЪаГЁЯњЪлЃЌЕЋCЪаГЁЕФЯњЪлзмСПВЛГЌЙ§5ЃЎ8ЖжЁБПЩЧѓГіxЕФШЁжЕЗЖЮЇЃЌдйНсКЯвЛДЮКЏЪ§ЕФаджЪПЩЧѓЕУНсТлЃЛ
ЃЈ3ЃЉЪзЯШИљОнЬтвтгУКЌгаmЕФДњЪ§ЪНБэЪОW=(300Ѓm)xЃЋ140000ЃЋ140mЃЌдйЧѓГіxЕФШЁжЕЗЖЮЇЮЊ50ЁмxЁм80ЃЌШЛКѓИљОнЗжРрЬжТлЕУГіmЕФжЕЃЎ
(1)ИљОнЬтвтЕУЃК WЃН1200xЃЋ1000(140Ѓx)ЃН200xЃЋ140000 ЃЎ
(2)ИљОнЬтвтЕУЃЌ 5%xЃЋ3%(140Ѓx) Ём5.8ЃЌНтЕУ xЁм80ЃЎ
Ёр0ЃМxЁм80ЃЎ
гжЁпдквЛДЮКЏЪ§WЃН200 x ЃЋ140000жаЃЌkЃН200ЃО0ЃЌ
ЁрWЫцxЕФдіДѓЖјдіДѓЃЌ
ЁрЕБx ЃН80ЪБЃЌWзюДѓЃН200ЁС80ЃЋ140000ЃН156000ЃЎ
ЁрНЋет140ЖжЪпВЫШЋВПЯњЪлЭъЃЌзюЖрПЩЛёЕУРћШѓ156000дЊЃЎ
(3)ИљОнЬтвтЃЌЕУWЃН(1200ЃЋ100)xЃЋ(1000ЃЋm)(140Ѓx)ЃН(300Ѓm)xЃЋ140000ЃЋ140mЃЎ
Ёп140ЃxЁм90ЃЌ
ЁрxЁн50ЃЌ
Ёр50ЁмxЁм80ЃЎ
ЂйЕБ300ЃmЃМ0ЃЌМД300ЃМmЃМ400ЪБЃЌWЫцxЕФдіДѓЖјМѕаЁЃЌ
ЁрЕБxЃН50ЪБЃЌWШЁзюДѓжЕЃЌДЫЪБWЃН50(300Ѓm)ЃЋ140000ЃЋ140mЃН179000ЃЌ
НтЕУmЃН![]() ЃЌ
ЃЌ
Ёп![]() ЃМ300ЃЌ
ЃМ300ЃЌ
ЁретжжЧщПіВЛЗћКЯЬтвтЃЛ
ЂкЕБ300ЃmЃН0ЃЌМДmЃН300ЪБЃЌWЃН182000ЃО179000ЃЌетжжЧщПіВЛЗћКЯЬтвтЃЛ
ЂлЕБ300ЃmЃО0ЃЌМД200ЃМmЃМ300ЪБЃЌWЫцxЕФдіДѓЖјдіДѓЃЌ
ЁрЕБxЃН80ЪБЃЌWШЁзюДѓжЕЃЌДЫЪБWЃН80(300Ѓm)ЃЋ140000ЃЋ140mЃН179000ЃЌ
НтЕУmЃН250ЃЎ
злЩЯПЩжЊmЃН250ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГХњЗЂЪаГЁгажаеаПМЪдЮФОпЬззАЃЌЦфжа![]() ЦЗХЦЕФХњЗЂМлЪЧУПЬз
ЦЗХЦЕФХњЗЂМлЪЧУПЬз![]() дЊЃЌ
дЊЃЌ![]() ЦЗХЦЕФХњЗЂМлЪЧУПЬз
ЦЗХЦЕФХњЗЂМлЪЧУПЬз![]() дЊЃЌаЁЭѕашЙКТђ
дЊЃЌаЁЭѕашЙКТђ![]() СНжжЦЗХЦЕФЮФОпЬззАЙВ
СНжжЦЗХЦЕФЮФОпЬззАЙВ![]() ЬзЃЎ
ЬзЃЎ
ЃЈ1ЃЉШєаЁЭѕАДашЙКТђ![]() СНжжЦЗХЦЮФОпЬззАЙВгУ
СНжжЦЗХЦЮФОпЬззАЙВгУ![]() дЊЃЌдђИїЙКТђЖрЩйЬзЃП
дЊЃЌдђИїЙКТђЖрЩйЬзЃП
ЃЈ2ЃЉЦОЛсдБПЈдкДЫХњЗЂЪаГЁЙКТђЩЬЦЗПЩвдЛёЕУ![]() елгХЛнЃЌЛсдБПЈЗбгУЮЊ
елгХЛнЃЌЛсдБПЈЗбгУЮЊ![]() дЊ.ШєаЁЭѕЙКТђЛсдБПЈВЂгУДЫПЈАДашЙКТђ
дЊ.ШєаЁЭѕЙКТђЛсдБПЈВЂгУДЫПЈАДашЙКТђ![]() ЬзЮФОпЬззАЃЌЙВгУСЫ
ЬзЮФОпЬззАЃЌЙВгУСЫ![]() дЊЃЎЩш
дЊЃЎЩш![]() ЦЗХЦЮФОпЬззАТђСЫ
ЦЗХЦЮФОпЬззАТђСЫ![]() АќЃЌЧыЧѓГі
АќЃЌЧыЧѓГі![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+cКЭжБЯпyЃНkx+bЖМОЙ§ЕуЃЈЉ1ЃЌ0ЃЉЃЌХзЮяЯпЕФЖдГЦжсЮЊxЃН1ЃЌФЧУДЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
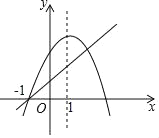
A.acЃО0
B.b2Љ4acЃМ0
C.kЃН2a+c
D.xЃН4ЪЧax2+ЃЈbЉkЃЉx+cЃМbЕФНт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌ![]() ЪЧ
ЪЧ![]() ЕФжБОЖЃЌ
ЕФжБОЖЃЌ![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() ЕФАыОЖ
ЕФАыОЖ![]() ЩЯдЫЖЏЃЌ
ЩЯдЫЖЏЃЌ![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЕФЧаЯпЃЌЧаЕуЮЊ
ЕФЧаЯпЃЌЧаЕуЮЊ![]() ЃЎ
ЃЎ
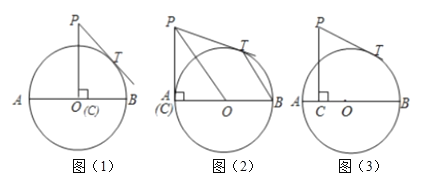
ЃЈ1ЃЉШчЭМЃЈ1ЃЉЃЌЕБ![]() ЕудЫЖЏЕН
ЕудЫЖЏЕН![]() ЕуЪБЃЌЧѓ
ЕуЪБЃЌЧѓ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ2ЃЉШчЭМЃЈ2ЃЉЃЌЕБ![]() ЕудЫЖЏЕН
ЕудЫЖЏЕН![]() ЕуЪБЃЌСЌНг
ЕуЪБЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМЃЈ3ЃЉЃЌЩш![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНМА
ЕФКЏЪ§ЙиЯЕЪНМА![]() ЕФзюаЁжЕЃЎ
ЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
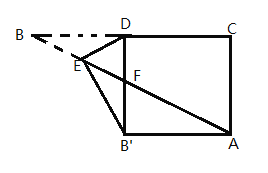
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌABЃН3![]() ЃЌBCЃН12ЃЌEЮЊADжаЕуЃЌFЮЊABЩЯвЛЕуЃЌНЋЁїAEFбиEFелЕўКѓЃЌЕуAЧЁКУТфЕНCFЩЯЕФЕуGДІЃЌдђелКлEFЕФГЄЪЧ_____ЃЎ
ЃЌBCЃН12ЃЌEЮЊADжаЕуЃЌFЮЊABЩЯвЛЕуЃЌНЋЁїAEFбиEFелЕўКѓЃЌЕуAЧЁКУТфЕНCFЩЯЕФЕуGДІЃЌдђелКлEFЕФГЄЪЧ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
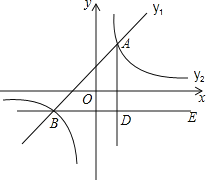
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓгыЗДБШР§КЏЪ§
ЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгкЕу
ЕФЭМЯѓНЛгкЕу![]() КЭ
КЭ![]() ЃЎ
ЃЎ
![]() ЧѓвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЧѓвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
![]() ЧыжБНгаДГі
ЧыжБНгаДГі![]() ЪБЃЌxЕФШЁжЕЗЖЮЇЃЛ
ЪБЃЌxЕФШЁжЕЗЖЮЇЃЛ
![]() Й§ЕуBзї
Й§ЕуBзї![]() жсЃЌ
жсЃЌ![]() гкЕуDЃЌЕуCЪЧжБЯпBEЩЯвЛЕуЃЌШє
гкЕуDЃЌЕуCЪЧжБЯпBEЩЯвЛЕуЃЌШє![]() ЃЌЧѓЕуCЕФзјБъЃЎ
ЃЌЧѓЕуCЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ12ЗжЃЉШчЭМ1ЃЌЕуOЪЧе§ЗНаЮABCDСНЖдНЧЯпЕФНЛЕуЃЌЗжБ№бгГЄODЕНЕуGЃЌOCЕНЕуEЃЌЪЙOG=2ODЃЌOE=2OCЃЌШЛКѓвдOGЁЂOEЮЊСкБпзїе§ЗНаЮOEFGЃЌСЌНгAGЃЌDEЃЎ

ЃЈ1ЃЉЧѓжЄЃКDEЁЭAGЃЛ
ЃЈ2ЃЉе§ЗНаЮABCDЙЬЖЈЃЌНЋе§ЗНаЮOEFGШЦЕуOФцЪБеыа§зЊІСНЧЃЈ0ЁуЃМІСЃМ360ЁуЃЉЕУЕНе§ЗНаЮOEЁфFЁфGЁфЃЌШчЭМ2ЃЎ
Ђйдка§зЊЙ§ГЬжаЃЌЕБЁЯOAGЁфЪЧжБНЧЪБЃЌЧѓІСЕФЖШЪ§ЃЛ
ЂкШєе§ЗНаЮABCDЕФБпГЄЮЊ1ЃЌдка§зЊЙ§ГЬжаЃЌЧѓAFЁфГЄЕФзюДѓжЕКЭДЫЪБІСЕФЖШЪ§ЃЌжБНгаДГіНсЙћВЛБиЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дк![]() жа.
жа.![]() ,
,![]() ,
,![]() ,Еу
,Еу![]() ЪЧ
ЪЧ![]() ЕФжаЕу,Еу
ЕФжаЕу,Еу![]() ЪЧБп
ЪЧБп![]() ЩЯвЛЖЏЕу,би
ЩЯвЛЖЏЕу,би![]() ЫљдкжБЯпАб
ЫљдкжБЯпАб![]() ЗелЕН
ЗелЕН![]() ЕФЮЛжУ,
ЕФЮЛжУ,![]() НЛ
НЛ![]() гкЕу
гкЕу![]() .Шє
.Шє![]() ЮЊжБНЧШ§НЧаЮ,дђ
ЮЊжБНЧШ§НЧаЮ,дђ![]() ЕФГЄЮЊ_______ЃЎ
ЕФГЄЮЊ_______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌФГЪ§бЇЛюЖЏаЁзщЮЊВтСПбЇаЃЦьИЫABЕФИпЖШЃЌбиЦьИЫе§ЧАЗН![]() УзДІЕФЕуCГіЗЂ,биаБУцЦТЖШ
УзДІЕФЕуCГіЗЂ,биаБУцЦТЖШ![]() ЕФаБЦТCDЧАНј4УзЕНДяЕуDЃЌдкЕуDДІАВжУВтНЧвЧЃЌВтЕУЦьИЫЖЅВПAЕФбіНЧЮЊ37ЁуЃЌСПЕУвЧЦїЕФИпDEЮЊ1.5Уз.вбжЊAЁЂBЁЂCЁЂDЁЂEдкЭЌвЛЦНУцФкЃЌABЁЭBC,AB//DE.ЧѓЦьИЫABЕФИпЖШ.ЃЈВЮПМЪ§ОнЃКsin37ЁуЁж
ЕФаБЦТCDЧАНј4УзЕНДяЕуDЃЌдкЕуDДІАВжУВтНЧвЧЃЌВтЕУЦьИЫЖЅВПAЕФбіНЧЮЊ37ЁуЃЌСПЕУвЧЦїЕФИпDEЮЊ1.5Уз.вбжЊAЁЂBЁЂCЁЂDЁЂEдкЭЌвЛЦНУцФкЃЌABЁЭBC,AB//DE.ЧѓЦьИЫABЕФИпЖШ.ЃЈВЮПМЪ§ОнЃКsin37ЁуЁж![]() ЃЌcos37ЁуЁж
ЃЌcos37ЁуЁж![]() ЃЌtan37ЁуЁж
ЃЌtan37ЁуЁж![]() .МЦЫуНсЙћБЃСєИљКХЃЉ
.МЦЫуНсЙћБЃСєИљКХЃЉ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com