
分析 根据绝对值得出函数y=|x-1|(-1≤x≤2)的解析式,再利用两直线相交解答即可.
解答 解:当-1≤x<1时,y=-x+1;
当2≥x≥1时,y=x-1;
因为函数y=|x-1|(-1≤x≤2)与y=$\frac{1}{2}$x+m的图象有两个交点,
可得:-x+1=$\frac{1}{2}$x+m(-1≤x<1)或x-1=$\frac{1}{2}$x+m(2≥x≥1),
解得:0<$\frac{1}{2}$x+m<1(-1≤x≤2),
解得:$-\frac{1}{2}<m<0$.
故答案为:$-\frac{1}{2}<m<0$.
点评 此题考查两直线相交问题,关键是根据绝对值得出函数y=|x-1|(-1≤x≤2)的解析式.


科目:初中数学 来源: 题型:填空题
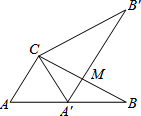 如图,△ABC中,∠ACB=90°,∠B=30°,BC=6,三角板绕C逆时针旋转,当点A的对应点A′落在AB边上时即停止转动,则BM的长为3.
如图,△ABC中,∠ACB=90°,∠B=30°,BC=6,三角板绕C逆时针旋转,当点A的对应点A′落在AB边上时即停止转动,则BM的长为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com