
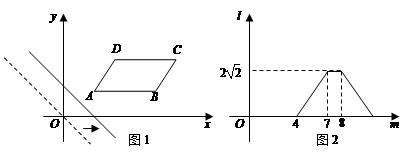
如 图1,在平面直角坐标系中,将□ABCD放置在第一象限,且AB∥x轴.直线y=-x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示,那么ABCD面积为( )
图1,在平面直角坐标系中,将□ABCD放置在第一象限,且AB∥x轴.直线y=-x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示,那么ABCD面积为( )
A.4 B.4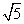 C.8 D.8
C.8 D.8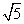
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:初中数学 来源: 题型:
铜陵学院毕业生小张响应国家“自主创业”的号召,投资开办了一个装饰品商店,该店采购进一种今年新上市的饰品进行了30天的试销售,购进价格为20元/件.销售结束后,得知日销售量P(件)与销售时间x(天)之间有如下关系: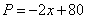 (1≤x≤30,且x为整数);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系:
(1≤x≤30,且x为整数);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系: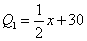 (1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数).
(1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数).
(1)第25天该商店的日销售利润为多少元?
(2)试写出该商店日销售利润y(元)关于销售时间x(天)之间的函数关系式;
(2)请问在这30天的试销售中,哪一天的日销售利润最大?并求出这个最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
草莓是我地区的特色时令水果,草莓一上市,水果店的老板用1200元购进一批草莓很快售完;老板又用2500元购进第二批草莓,所购箱数是第一批的2倍,但进价比第一批每箱多了5元.
(1)第一批草莓每箱进价多少元?
(2)老板以每箱150元的价格销售第二批草莓,售出80%后,为了尽快售完,决定打折促销,要使第二批草莓的销售利润不少于320元,剩余的草莓每箱售价至少打几折? (利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
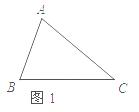
1)如图1,已知△ABC,以AB,AC为边向△AB C外做等边△ABD和等边△ACE.连接BE,CD.请你完成图形,并证明:BE=CD;(尺规作图,不写做法,保留作图痕迹)
C外做等边△ABD和等边△ACE.连接BE,CD.请你完成图形,并证明:BE=CD;(尺规作图,不写做法,保留作图痕迹)
(2)如图2,已知△ABC,以AB,AC为边向外做正方形ABFD和正方形ACGE.连接BE,CD.BE与CD有什么数量关系?简单说明理由.

(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:
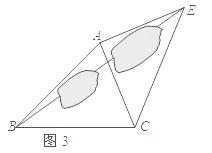
如图3,要测量池塘两岸相对的两点B,E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=10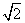 米,AC=AE.求BE的长.
米,AC=AE.求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,矩形AEHC是由三个全等矩形拼成的,AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N,设△BPQ, △DKM, △CNH 的面积依次为S1,S2,S3.若S1+S3=20,则S2的值为( ).
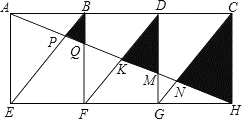
A.6 B. 8 C. 10 D. 12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com