
如图,矩形AEHC是由三个全等矩形拼成的,AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N,设△BPQ, △DKM, △CNH 的面积依次为S1,S2,S3.若S1+S3=20,则S2的值为( ).
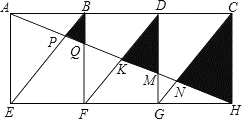
A.6 B. 8 C. 10 D. 12
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
中国象棋红方棋子按兵种不同分布如下:1个帅,5个兵,“士、象、马、车、炮”各两个,将所有棋子反面朝上放在棋盘中,任取一个不是士、象、帅的概率是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
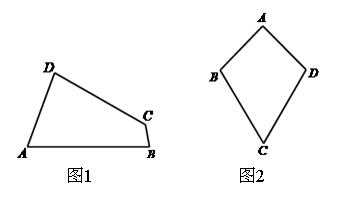
(1)已知:如图1,四边形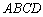 是“等对角四边形”,
是“等对角四边形”,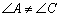 ,
,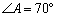 ,
, .求
.求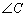 ,
,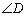 的度数.
的度数.
(2)在探究“等对角四边形”性质时:
① 小红画了一个“等对角四边形”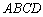 (如图2),其中
(如图2),其中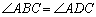 ,
,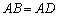 ,此时她发现
,此时她发现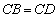 成立.请你证明此结论.
成立.请你证明此结论.
② 由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
(3)已知:在“等对角四边形”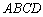 中,
中, ,
,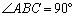 ,
,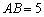 ,
,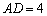 .求对角线
.求对角线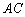 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
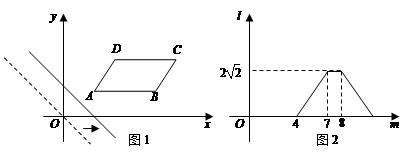
如 图1,在平面直角坐标系中,将□ABCD放置在第一象限,且AB∥x轴.直线y=-x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示,那么ABCD面积为( )
图1,在平面直角坐标系中,将□ABCD放置在第一象限,且AB∥x轴.直线y=-x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示,那么ABCD面积为( )
A.4 B.4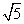 C.8 D.8
C.8 D.8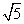
查看答案和解析>>
科目:初中数学 来源: 题型:
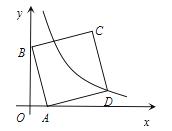
如图,在平面直角坐标系中,A(1,0),B(0,3),以AB为边在第一象限作正方形ABCD,点D在双曲线y=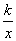 (k≠0)上,将正方形沿x轴负方向平移 m个单位长度后,点C恰好落在双曲线上,则m的值是
(k≠0)上,将正方形沿x轴负方向平移 m个单位长度后,点C恰好落在双曲线上,则m的值是
查看答案和解析>>
科目:初中数学 来源: 题型:
某五金店购进 一批数量足够多的p型节能电灯 进价为35元/只,以50元/只销售,每天销售20只.市场调研发现:若每只每降l元,则每天销售数量比原来多3只.现商店决定对Q型节能电灯进行降价促销活动,每只降价x元(x为正整数).在促销期间,商店要想每天获得最大销售利润,每只应降价多少元?每天最大销售毛利润为多少?(注:每只节能灯的销售毛利润指每只节能灯的销售价与进货价的差)
一批数量足够多的p型节能电灯 进价为35元/只,以50元/只销售,每天销售20只.市场调研发现:若每只每降l元,则每天销售数量比原来多3只.现商店决定对Q型节能电灯进行降价促销活动,每只降价x元(x为正整数).在促销期间,商店要想每天获得最大销售利润,每只应降价多少元?每天最大销售毛利润为多少?(注:每只节能灯的销售毛利润指每只节能灯的销售价与进货价的差)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在矩形纸片ABCD中,AB=5CM,BC=10CM,CD上有一点E,ED=2cm,AD上有一点P,PD=3cm,过点P作PF⊥AD,交BC于点F,将纸片折叠,使点P与点E重合,折痕与PF交于点Q,则PQ的长是( ).

A.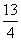 cm B.3cm C.2cm D.
cm B.3cm C.2cm D.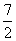 cm
cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com