练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在矩形纸片ABCD中，AB=5CM，BC=10CM，CD上有一点E，ED=2cm，AD上有一点P，PD=3cm，过点P作PF⊥AD，交BC于点F，将纸片折叠，使点P与点E重合，折痕与PF交于点Q，则PQ的长是(    ).

    A.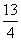 cm     B.3cm     C.2cm     D.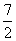cm


    A.

    【解析】过Q点作QG⊥CD，垂足为G点，连接QE，设PQ=x，由折叠及矩形的性质可知，

    EQ=PQ=x，QG=PD=3，EG=x-2，在Rt△EGQ中，由勾股定理得：EG2+GQ2=EQ2，即：（x-2）2+32=x2，解得：x=，即PQ=.

    故选A.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    下列图案由正多边形拼成，其中既是轴对称图形又是中心对称图形的是（  ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，矩形AEHC是由三个全等矩形拼成的，AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N，设△BPQ, △DKM, △CNH 的面积依次为S1，S2，S3.若S1+S3=20，则S2的值为(     )．

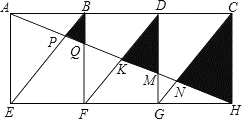
    A．6       B. 8       C. 10      D. 12

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    操作：小英准备制作一个表面积为6cm2的正方体纸盒，现选用一些废弃的纸片进行如下设计：

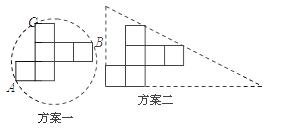
    说明：

    方案一：图形中的圆过点A.B.C；

    方案二：直角三角形的两直角边与展开图左下角的正方形边重合，斜边经过两个正方形的顶点．

    纸片利用率=×100%

    发现：（1）小英发现方案一中的点A.B恰好为该圆一直径的两个端点．你认为小英的这个发现是否正确，请说明理由．

    （2）小英通过计算，发现方案一中纸片的利用率仅约为38.2%．请帮忙计算方案二的利用率，并写出求解过程．（结果精确到0.1%）

    探究：（3）小英感觉上面两个方案的利用率均偏低，又进行了新的设计（方案三），请直接写出方案三的利用率．（结果精确到0.1%）

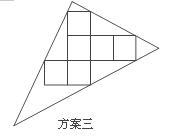
    说明：方案三中的每条边均过其中两个正方形的顶点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，和都是等腰直角三角形，,反比例函数y=在第一象限的图象经过点B，若，则k的值为（    ）

    A．4         B．6            C．8        D．12

    查看答案和解析>>

    科目：初中数学 来源： 题型：


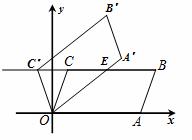
    如图，在平面直角坐标系xOy中，□OABC的顶点A、B的坐标分别为（6，0）、（7，3），将□OABC绕点O逆时针方向旋转得到□O，当点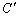落在BC的延长线上时，线段交BC于点E，则线段的长度为       ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


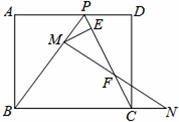
    如图，矩形ABCD中，AD=10，AB=8，点P在边CD上，且BP=BC，点M在线段BP上，点N在线段BC的延长线上，且PM=CN，连接MN交BP于点F，过点M作ME⊥CP于E，则EF=        .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    设，且1－ab2≠0，则=          .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在同一直角坐标系下，直线y=x+2与双曲线的交点的个数为【    】

    　　A．0个　　B．1个　　C．2个　　D．不能确定

    查看答案和解析>>

    同步练习册答案