


 操作:小英准备制作一个表面积为6cm2的正方体纸盒,现选用一些废弃的纸片进行如下设计:
操作:小英准备制作一个表面积为6cm2的正方体纸盒,现选用一些废弃的纸片进行如下设计:
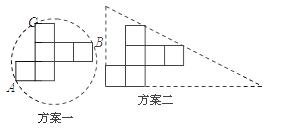
说明:
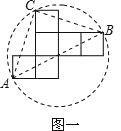
方案一:图形中的圆过点A.B.C;
方案二:直角三角形的两直角边与展开图左下角的正方形边重合,斜边经过两个正方形的顶点.
纸片利用率= ×100%
×100%
发现:(1)小英发现方案一中的点A.B恰好为该圆一直径的两个端点.你认为小英的这个发现是否正确,请说明理由.
(2)小英通过计算,发现方案一中纸片的利用率仅约为38.2%.请帮忙计算方案二的利用率,并写出求解过程.(结果精确到0.1%)
探究:(3)小英感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.(结果精确到0.1%)
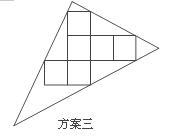
说明:方案三中的每条边均过其中两个正方形的顶点.
(1)小英的这个发现正确,理由略;(2)37.5% ;(3)49.9% ;
【解析】发现:(1)小英的这个发现正确.
理由:解法一:如图一:连接AC、BC、AB,∵AC=BC=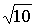 ,AB=2
,AB=2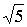 ,∴AC2+BC2=AB2,∴∠ACB=90°,∴AB为该圆的直径.
,∴AC2+BC2=AB2,∴∠ACB=90°,∴AB为该圆的直径.
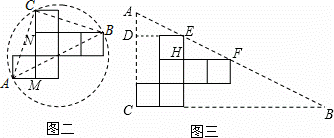
解法二:如图二:连接AC、BC、AB.易证△AMC≌△BNC,∴∠ACM=∠CBN.
又∵∠BCN+∠CBN=90°,∴∠BCN+∠ACM=90°,即∠BAC=90°,∴AB为该圆的直径.
(2)如图三:∵DE=FH,DE∥FH,∴∠AED=∠EFH,
∵∠ADE=∠EHF=90°,∴△ADE≌△EHF(ASA),∴AD=EH=1.
∵DE∥BC,∴△ADE∽△ACB,∴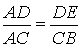 ,∴
,∴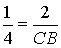 ,∴BC=8,∴S△ACB=16.
,∴BC=8,∴S△ACB=16.
∴该方案纸片利用率=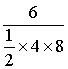 ×100%=37.5%;
×100%=37.5%;
探究:(3)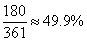 .
.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
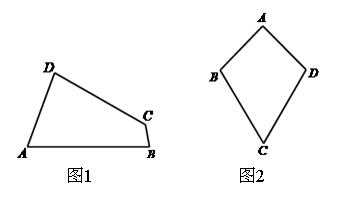
(1)已知:如图1,四边形 是“等对角四边形”,
是“等对角四边形”,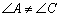 ,
,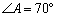 ,
, .求
.求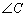 ,
,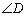 的度数.
的度数.
(2)在探究“等对角四边形”性质时:
① 小红画了一个“等对角四边形”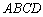 (如图2),其中
(如图2),其中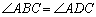 ,
,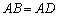 ,此时她发现
,此时她发现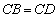 成立.请你证明此结论.
成立.请你证明此结论.
② 由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
(3)已知:在“等对角四边形”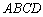 中,
中, ,
,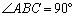 ,
,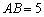 ,
,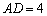 .求对角线
.求对角线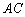 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
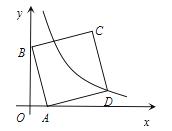
如图,在平面直角坐标系中,A(1,0),B(0,3),以AB为边在第一象限作正方形ABCD,点D在双曲线y=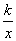 (k≠0)上,将正方形沿x轴负方向平移 m个单位长度后,点C恰好落在双曲线上,则m的值是
(k≠0)上,将正方形沿x轴负方向平移 m个单位长度后,点C恰好落在双曲线上,则m的值是
查看答案和解析>>
科目:初中数学 来源: 题型:
某五金店购进 一批数量足够多的p型节能电灯 进价为35元/只,以50元/只销售,每天销售20只.市场调研发现:若每只每降l元,则每天销售数量比原来多3只.现商店决定对Q型节能电灯进行降价促销活动,每只降价x元(x为正整数).在促销期间,商店要想每天获得最大销售利润,每只应降价多少元?每天最大销售毛利润为多少?(注:每只节能灯的销售毛利润指每只节能灯的销售价与进货价的差)
一批数量足够多的p型节能电灯 进价为35元/只,以50元/只销售,每天销售20只.市场调研发现:若每只每降l元,则每天销售数量比原来多3只.现商店决定对Q型节能电灯进行降价促销活动,每只降价x元(x为正整数).在促销期间,商店要想每天获得最大销售利润,每只应降价多少元?每天最大销售毛利润为多少?(注:每只节能灯的销售毛利润指每只节能灯的销售价与进货价的差)
查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①a,b同号;②当x=1和x=3时,函数值相等;③4a+b=0;④当y=-2时,x的值只能为0,其中正确的个数是( )
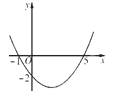
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在矩形纸片ABCD中,AB=5CM,BC=10CM,CD上有一点E,ED=2cm,AD上有一点P,PD=3cm,过点P作PF⊥AD,交BC于点F,将纸片折叠,使点P与点E重合,折痕与PF交于点Q,则PQ的长是( ).

A.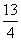 cm B.3cm C.2cm D.
cm B.3cm C.2cm D.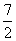 cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB是⊙O的直径,OD垂直于弦AC于点E,且交⊙O于点D,F是BA延长线上一点,若∠CDB=BFD.
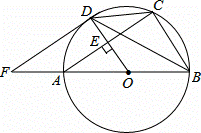
(1)求证:FD是⊙O的一条切线;
(2)若AB=10,AC=8,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
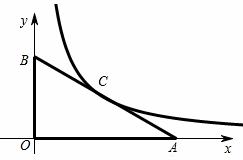
如图,Rt△OAB的边OA在x 轴的正半轴上,OB在y轴的正半轴上,双曲线
轴的正半轴上,OB在y轴的正半轴上,双曲线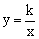 过AB的中点C,已知点A的坐标为(
过AB的中点C,已知点A的坐标为( ,0),点B的坐标
,0),点B的坐标 为(0,1),则该双曲线的表达式为【 】
为(0,1),则该双曲线的表达式为【 】

A. B.
B. C.
C.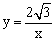 D.
D.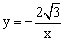
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com