练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，AB是⊙O的直径，OD垂直于弦AC于点E，且交⊙O于点D，F是BA延长线上一点，若∠CDB=BFD．

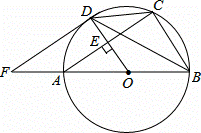
    （1）求证：FD是⊙O的一条切线；

    （2）若AB=10，AC=8，求DF的长．


    （1）证明见解析；（2）．

    【解析】（1）∵∠CDB=∠CAB，∠CDB=∠BFD，∴∠CAB=∠BFD，∴FD∥AC，∵∠AEO=90°，∴∠FDO=90°，∴FD是⊙O的一条切线；

    (2)∵AB=10，AC=8，DO⊥AC，∴AE=EC=4，AO=5，∴EO=3，∵AE∥FD，∴△AEO∽△FDO，

    ∴，∴，解得：FD=．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    某书店把一本新书按标价的九折出售，仍可获利20%．若该书的进价为21元，则标价为        元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    操作：小英准备制作一个表面积为6cm2的正方体纸盒，现选用一些废弃的纸片进行如下设计：

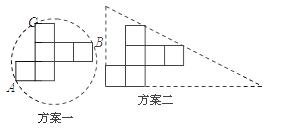
    说明：

    方案一：图形中的圆过点A.B.C；

    方案二：直角三角形的两直角边与展开图左下角的正方形边重合，斜边经过两个正方形的顶点．

    纸片利用率=×100%

    发现：（1）小英发现方案一中的点A.B恰好为该圆一直径的两个端点．你认为小英的这个发现是否正确，请说明理由．

    （2）小英通过计算，发现方案一中纸片的利用率仅约为38.2%．请帮忙计算方案二的利用率，并写出求解过程．（结果精确到0.1%）

    探究：（3）小英感觉上面两个方案的利用率均偏低，又进行了新的设计（方案三），请直接写出方案三的利用率．（结果精确到0.1%）

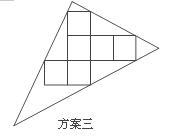
    说明：方案三中的每条边均过其中两个正方形的顶点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


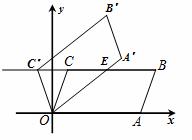
    如图，在平面直角坐标系xOy中，□OABC的顶点A、B的坐标分别为（6，0）、（7，3），将□OABC绕点O逆时针方向旋转得到□O，当点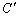落在BC的延长线上时，线段交BC于点E，则线段的长度为       ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


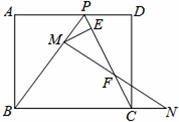
    如图，矩形ABCD中，AD=10，AB=8，点P在边CD上，且BP=BC，点M在线段BP上，点N在线段BC的延长线上，且PM=CN，连接MN交BP于点F，过点M作ME⊥CP于E，则EF=        .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图1，已知三角形ABC中，AB=BC=1，∠ABC=90度，把一块含30度角的三角板DEF的直角顶点D放在AC的中点上，将直角三角板DEF绕D点按逆时针方向旋转。

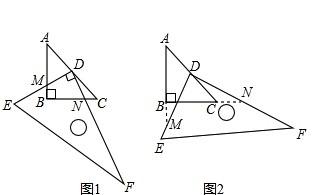
    （1）在图1中，DE交AB于M，DF交BC于N.

    ①直接写出DM、DN的数量关系；

    ②在这一过程中，直角三角板DEF与三角形ABC的重叠部分为四边形DMBN，请说明四边形DMBN的面积是否发生变化？若发生变化，请说明如何变化的；若不发生变化，请求出其面积.

    （2）继续旋转至如图2的位置，延长AB交DE于M，延长BC交DF于N，DM=DN是否仍然成立？若成立，请给出证明；若不成立，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    设，且1－ab2≠0，则=          .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在“老年节” 前夕，某公司工会组织323名退休职工到浙江杭州旅游，旅游前，工会确定每车保证有一名随团医生，并为此次旅游请了8名医生，现打算同时租甲、乙两种客车，其中甲种客车每辆载客50人，乙种客车每辆载客20人。

    （1）请帮助工会设计租车方案。

    （2）若甲种客车租金为800元/辆，乙种客车租金为600元/辆，工会按哪种方案租车最省钱？此时租金是多少？

    （3）旅游前，一名医生由于有特殊情况，工会只能安排7名医生随团，为保证所租的每辆车安排有一名医生，租车方案调整为：同时租80座、50座和20座的大小三种客车，出发时，所租的三种客车的座位恰好坐满，请问工会的租车方案如何安排？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知二次函数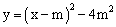（m＞0）的图象与x轴交于A、B两点．

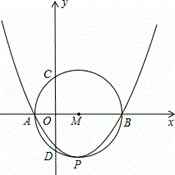
    （1）写出A、B两点的坐标（坐标用m表示）；

    （2）若二次函数图象的顶点P在以AB为直径的圆上，求二次函数的解析式；

    （3）设以AB为直径的⊙M与y轴交于C、D两点，求CD的长．

    查看答案和解析>>

    同步练习册答案