
分析 根据直角三角形中两锐角互余和锐角三角函数可解答问题.
解答 解:(1)∵在Rt△ABC中,∠C=90°,b=2$\sqrt{3}$,c=4,
∴a=$\sqrt{{c}^{2}-{b}^{2}}=\sqrt{{4}^{2}-(2\sqrt{3})^{2}}=\sqrt{16-12}$=$\sqrt{4}$=2.
∴tanA=$\frac{a}{b}=\frac{2}{2\sqrt{3}}=\frac{\sqrt{3}}{3}$,tanB=$\frac{b}{a}=\frac{2\sqrt{3}}{2}=\sqrt{3}$.
∴∠A=30°,∠B=60°.
即a=2,∠A=30°,∠B=60°.
(2)∵在Rt△ABC中,∠C=90°,∠A=30°,b=8$\sqrt{3}$,
∴∠B=∠C-∠A=60°.
∵tanA=$\frac{a}{b}$,sinB=$\frac{b}{c}$.
∴a=8,c=16.
即∠B=30°,a=8,c=16.
(3)∵在Rt△ABC中,∠C=90°,c=8,∠A=60°,
∴∠B=∠C-∠A=30°.
∵sinA=$\frac{a}{c}$,sinB=$\frac{b}{c}$,c=8,
∴a=4$\sqrt{3}$,b=4.
即∠B=30°,a=4$\sqrt{3}$,b=4.
点评 本题考查解直角三角函数,解题的关键是明确锐角三角函数,找出所求问题需要需要的条件.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:解答题
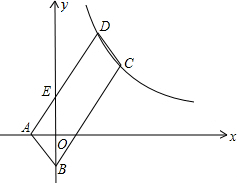 如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-2),顶点C、D在双曲线y=$\frac{k}{x}$上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的3倍.
如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-2),顶点C、D在双曲线y=$\frac{k}{x}$上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的3倍.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
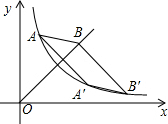 如图,已知反比例函数y=$\frac{k}{x}$(x>0)与正比例函数y=x(x≥0)的图象,点A(1,4),点A′(4,b)与点B′均在反比例函数的图象上,点B在直线y=x上,四边形AA′B′B是平行四边形,求B点坐标.
如图,已知反比例函数y=$\frac{k}{x}$(x>0)与正比例函数y=x(x≥0)的图象,点A(1,4),点A′(4,b)与点B′均在反比例函数的图象上,点B在直线y=x上,四边形AA′B′B是平行四边形,求B点坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com