
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,其顶点为
,其顶点为![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() .
.

(1)求点![]() 的坐标;
的坐标;
(2)直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 的面积等于
的面积等于![]() 的面积的3倍?若存在,求出点
的面积的3倍?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】“我要上春晚”进入决赛阶段,最终将有甲、乙、丙、丁4名选手进行决赛的终极较量,决赛分3期进行,每期比赛淘汰1名选手,最终留下的歌手即为冠军.假设每位选手被淘汰的可能性都相等.
(1)甲在第1期比赛中被淘汰的概率为 ;
(2)用树状图法或表格法求甲在第2期被淘汰的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组根据学习函数的经验,对分段函数y=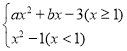 的图象与性质进了探究,请补充完整以下的探索过程.
的图象与性质进了探究,请补充完整以下的探索过程.
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 3 | 0 | ﹣1 | 0 | 1 | 0 | ﹣3 | … |
(1)填空:a= .b= .
(2)①提上述表格补全函数图象;②该函数图象是关于 对称的 (横线上填轴对称或中心对称)图形.
(3)若直线y=![]() x+t与该函数图象有三个交点,直接写出t的取值范围.
x+t与该函数图象有三个交点,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A,B的坐标分别为(1,0),(2,0).若二次函数y=x2+(a﹣3)x+3的图象与线段AB只有一个交点,则a的取值范围是_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
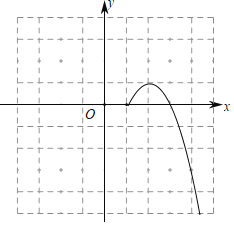
【题目】某一房间内A、B两点之间设有探测报警装置,小车(不计大小)在房间内运动,当小车从AB之间经过时,将触发报警.现将A、B两点放置于平面直角坐标系xOy中(如图),已知点A,B的坐标分别为(0,4),(4,4),小车沿抛物线y=ax2﹣2ax﹣3a(a<0)运动.若小车在运动过程中只触发一次报警装置,则a的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
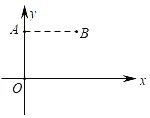
【题目】如图1,点A在x轴的负半轴上,点B的坐标为(﹣2,﹣4),抛物线y=ax2+bx的对称轴为x=﹣5,该抛物线经过点A、B,点E是AB与对称轴x=﹣5的交点.
(1)如图1,点P为直线AB下方的抛物线上的任意一点,在对称轴x=﹣5上有一动点M,当△ABP的面积最大时,求|PM﹣OM|的最大值以及点P的坐标.
(2)如图2,把△ABO沿射线BA方向平移,得到△CDF,其中点C、D、F分别是点A、B、O的对应点,且点F与点O不重合,平移过程中,是否存在这样的点F,使得以点A、E、F为顶点的三角形为等腰三角形?若存在,直接写出点F的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
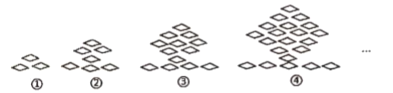
【题目】下列图形都是由同样大小的菱形按照一定规律组成的,其中图①有3个小菱形,图②有7个小菱形,图③有13个小菱形……请根据排列规律完成下列问题:
(1)请写出图⑤中小菱形的个数;
(2)根据表中规律猜想,图![]() 中小菱形的个数
中小菱形的个数![]() 与
与![]() 的关系式(不用说理);
的关系式(不用说理);
(3)是否存在一个图形恰好由91个菱形组成?若存在,求出图形的序号;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知:![]() ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么![]() ABCD的周长是多少?
ABCD的周长是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com