
����Ŀ����ƽ��ֱ������ϵxOy�У���M������Ϊ��x1��y1�����������Ϊ��x2��y2������x1��x2��y1��y2����MNΪ�߹������Σ��������ε������ԽǷ�ƽ����x�ᡢy�ᣬ��Ƹ�����Ϊ�ߵġ��������Ρ���

��1����֪��A��2��0����B��0��3��������ABΪ�ߵġ��������Ρ������Ϊ�� ����
��2������C��1��2������D��ֱ��x��5�ϣ���CDΪ�ߵġ��������Ρ�Ϊ�����Σ���ֱ��CD�ĺ�������ʽ��
���𰸡���1��12����2��y��x+1��y����x+3
��������
��1�����ݶ��彨����ABΪ�ߵ�����������������������������ɣ�
��2����ȷ��ֱ��CD��ֱ��y=5�ļн���45�㣬��D��5��6����5����2�������ô���ϵ������ֱ��CD����ʽ.
�⣺��1����ͼ1��
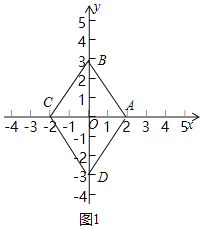
�ߵ�A��2��0����B��0��3����
��OA��2��OB��3��
���ı���ABCD������
��AC��2OA��4��BD��2OB��6��
����ABΪ�ߵġ��������Ρ��������![]() AC��BD��12��
AC��BD��12��
�ʴ�Ϊ��12
��2����ͼ2��
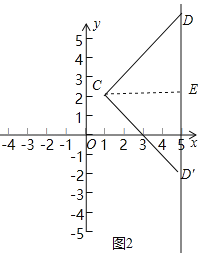
����CDΪ�ߵġ��������Ρ�Ϊ�����Σ�
��ֱ��CD��ֱ��x��5�ļн���45�㣬
����C��CE��DE��E��
��D��5��6����5����2����
��ֱ��CD�Ľ���ʽΪy��kx+b��
![]() ��
��![]()
��![]() ��
��![]()
��ֱ��CD�ı���ʽΪ��y��x+1��y����x+3��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
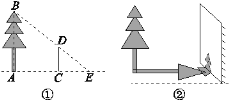
����Ŀ��Ϊ�˲���ͼ�٢��е���������ͬһʱ��ij�˽��������²�����
ͼ�٣�������CD�ij�Ϊ0.8������Ӱ��CEΪ1������ӰAE��Ϊ2.4�ף�
ͼ�ڣ�������ڵ����ϵ�����Ӱ��Ϊ2.8��������ǽ�ϵ���Ӱ��1.2�ף�
����ͼ�ٺ�ͼ���е����߸��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(10�֣�ѧУ��֯ѧ���μ��ۺ�ʵ��������Dz�����ij��Ʒ���˶�Ь�����۹�������֪���˶�Ьÿ˫�Ľ���Ϊ120Ԫ��ΪѰ����ʵ����ۼ۸������4�������������������±���ʾ��
��1�� | ��2�� | ��3�� | ��4�� | |
�ۼ�x��Ԫ/˫�� | 150 | 200 | 250 | 300 |
������y��˫�� | 40 | 30 | 24 | 20 |
��1���۲�������ݣ�x��y����ʲô������ϵ����������������ϵʽ��
��2�����̳��ƻ�ÿ�����������Ϊ3000Ԫ�����䵥�۶�Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������6��־Ը�ߣ��ڡ�ʮһ��������֯���ڵ�δ����ѧ���������Σ�������ƱΪÿ��40Ԫ�����������Żݷ�����������־Ը����ѣ�δ����ѧ����8���շѣ��ҷ�����־Ը�ߺ�δ����ѧ������7���շѣ�����![]() ��δ����ѧ����
��δ����ѧ����
��1����![]() ʱ�������� Ԫ���ҷ����� Ԫ��
ʱ�������� Ԫ���ҷ����� Ԫ��
��2���ú�![]() ��ʽ�ӱ�ʾ���ַ����������Ԫ��
��ʽ�ӱ�ʾ���ַ����������Ԫ��
��3����![]() Ϊ��ֵʱ���ס������ַ�����һ���ģ�
Ϊ��ֵʱ���ס������ַ�����һ���ģ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ľ����������������Ӧ�����IJ�ľ���ֵ��������ͼ��ʾ����![]() �������Ϸֱ��Ӧ����Ϊ
�������Ϸֱ��Ӧ����Ϊ![]() ����
����![]() �����ľ����ʾΪ
�����ľ����ʾΪ![]() ��
��
![]()
��������֪ʶ���⣺
��1��������������![]() ��ʾ�����ֱ�Ϊ
��ʾ�����ֱ�Ϊ![]() ��
��
�ٵ�![]() ʱ��
ʱ��![]() ֮��ľ���Ϊ ��
֮��ľ���Ϊ ��
��![]() ֮��ľ�����ú�
֮��ľ�����ú�![]() ��ʽ�ӱ�ʾΪ
��ʽ�ӱ�ʾΪ![]() ��
��
����������֮��ľ���Ϊ2����ô![]() ֵΪ ��
ֵΪ ��
��2��![]() ����СֵΪ ����ʱ
����СֵΪ ����ʱ![]() ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��
��3����![]() ����
����![]() ����СֵΪ ��
����СֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽ⱾУ���꼶ѧ���Ŀ�����Ȥ���������С�������꼶һ����ͬѧ�Ŀ�����Ȥ���ý�����һ�ε��飬�����ݲɼ��������ݣ�������ͼ�ٺ�ͼ������ͳ��ͼ��
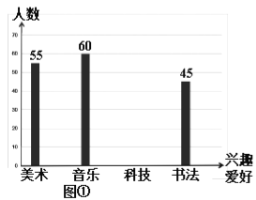
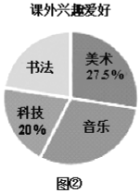
�������ͼ���ṩ����Ϣ���ش��������⣺
��1����ͼ���У������Ƽ������ֵ�ͼ����������
��2����ͼ���У��鷨��Բ�ĽǶ����Ƕ��٣�
��3�����ѧУ���꼶����300�ˣ���������ѧУ���꼶ѧ��������Ȥ���������ֺ������Ĺ��ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�Ķ���A�ǵȱ���EFG��FG���е㣬��B=60����EF=2������Ӱ���ֵ����Ϊ��������
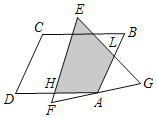
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O�ǵȱ�������ABC�����Բ��PΪ�ӻ�BC��һ��(��P���B��C���غ�)��
(1)���P���ӻ�BC���е㣬��֤��PB��PC��PA��
(2)����P���ӻ�BC���ƶ�ʱ��(1)�еĽ��ۻ���������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
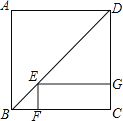
����Ŀ������ͼ����������![]() �У�
�У�![]() �ǶԽ�����
�ǶԽ�����![]() ����һ�㣬��
����һ�㣬��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ����������
����������![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() �����ı���
�����ı���![]() ���ܳ�Ϊ________
���ܳ�Ϊ________
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com