
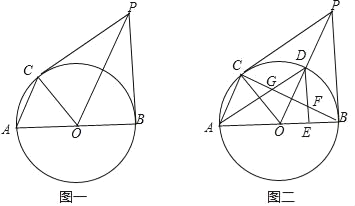
【题目】如图一,AB为⊙O直径,PB为⊙O切线,点C在⊙O上,弦AC∥OP.
(1)求证:PC为⊙O的切线.
(2)如图二,OP交⊙O于D,DA交BC于G,作DE⊥AB于E,交BC于F,若CG=3,DF=![]() ,求AC的长.
,求AC的长.
【答案】(1)证明见解析;(2)AC=6.
【解析】
(1)连OC,由AC∥OP,得到∠BOP=∠OAC,∠POC=∠OCA,则∠BOP=∠POC,可得△POB≌△POC,得到∠PBO=∠PCO,而PB为⊙O的切线,得∠OBP=90°,所以∠PCO=90°,根据切线的判定即可得到PC为⊙O的切线;
(2)连BD,由AB为⊙O的直径,得∠ADB=90°,而DE⊥AB,则∠BDE=∠BAD,所以∠BDE=∠BAD,从而易得到∠DBG=∠BDF,有BF=DF=FG=![]() ,BC=8,得到BH=
,BC=8,得到BH=![]() ,BC=8.易证Rt△BOH≌Rt△DOE,得DE=BH=8,则EF=DE-DF=8-5=3,在Rt△BEF中,利用勾股定理可求得BE=4,在Rt△DOE中,利用勾股定理即可得到⊙O的半径于是得到直径,根据勾股定理得到AC,于是得到结论.
,BC=8.易证Rt△BOH≌Rt△DOE,得DE=BH=8,则EF=DE-DF=8-5=3,在Rt△BEF中,利用勾股定理可求得BE=4,在Rt△DOE中,利用勾股定理即可得到⊙O的半径于是得到直径,根据勾股定理得到AC,于是得到结论.
(1)连OC,如图,
∵AC∥OP,
∴∠BOP=∠OAC,∠POC=∠OCA,
∵OA=OC,即∠OCA=∠OAC,
∴∠BOP=∠POC,
在△POB与△POC中,
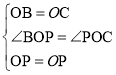
∴△POB≌△POC(SAS),
∴∠PBO=∠PCO,
而PB为⊙O的切线,
∴∠OBP=90°,
∴∠PCO=90°,
∴PC为⊙O的切线;
(2)连BD,
∵AB为⊙O的直径,
∴∠ADB=90°,
而DE⊥AB,
∴∠BDE=∠BAD,
由(1)得∠BOP=∠COP,
∴∠BAD=∠DBF,
∴∠DBG=∠BDF,
∵∠DBG+∠DGF=90°,∠BDF+∠GDF=90°,
∴∠FGD=∠FDG,
∴BF=DF=FG=![]() ,
,
∵∠ADE+∠DAE=∠AGF+∠CAG=∠CAG+∠DGF=90°,
∴∠ADE=∠DGF,
∴DF=GF,
∴BC=![]() +
+![]() +3=8,
+3=8,
∵OC=OB,PC=PB,
∴OP垂直平分线段BC,
∴BH=![]() BC=4,
BC=4,
在Rt△BOH与Rt△DOE中,
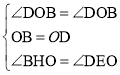
∴Rt△BOH≌Rt△DOE(ASA),
∴DE=BH=4.
∴EF=DE﹣DF=![]() ,
,
在Rt△BEF中,BE=![]() =2,
=2,
设⊙O半径为r,在Rt△DOE中,r2=42+(r﹣2)2.
∴r=5.
∴AB=10,
∴AC=![]() =6.
=6.



科目:初中数学 来源: 题型:
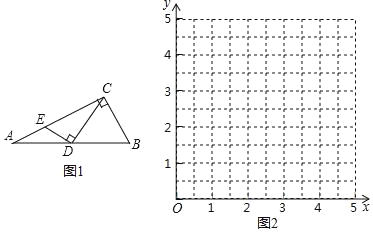
【题目】如图1,Rt△ABC中,∠ACB=90°,点D为AB边上的动点(点D不与点A,点B重合),过点D作ED⊥CD交直线AC于点E,已知∠A=30°,AB=4cm,在点D由点A到点B运动的过程中,设AD=xcm,AE=ycm.
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | … |
| 1 |
| 2 |
| 3 |
| … |
y/cm | … | 0.4 | 0.8 | 1.0 |
| 1.0 | 0 | 4.0 | … |
(说明:补全表格时相关数值保留一位小数)
(2)在如图2的平面直角坐标系xOy中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当AE=![]() AD时,AD的长度约为 cm.
AD时,AD的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
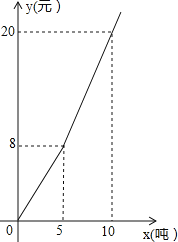
【题目】浙江实施“五水共治“以来,越来越重视节约用水,某地对居民用水按阶梯水价方式进行收费,人均月生活用水收费标准如图所示,图中x表示人均月生活用水的吨数,y表示收取的人均月生活用水费(元),请根据图象信息,回答下列问题.
(1)请写出y与x的函数关系式;
(2)若某个家庭有5人,响应节水号召,计划控制1月份的生活用水费不超过76元,则该家庭这个月最多可以用多少吨水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店准备销售一种多功能旅行背包,计划从厂家以每个120元的价格进货.

(1)经过市场调查发现,当每个背包的售价为140元时,月均销量为980个,售价每增长10元,月均销量就相应减少30个,若使这种背包的月均销量不低于800个,每个背包售价应不高于多少元?
(2)在实际销售过程中,由于原材料涨价和生产成本增加的原因,每个背包的进价为150元,而每个背包的售价比(1)中最高售价减少了a%(a>0),月均销量比(1)中最低月均销量800个增加了5a%,结果该店销售该背包的月均利润达到了40000元,求在实际销售过程中每个背包售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:“四个顶点都在三角形边上的正方形是三角形的内接正方形”.已知:在Rt△ABC中,∠C=90°,AC=6,BC=3.
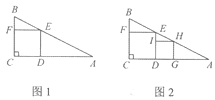
(1)如图l,四边形CDEF是△ABC的内接正方形,则正方形CDEF的边长a1是________;
(2)如图2,四边形DGHI是(1)中△EDA的内接正方形,那么第2个正方形DGHI的边长记为a2;继续在图2中的△HGA中按上述方法作第3个内接正方形……以此类推,则第n个内接正方形的边长an=____. (n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
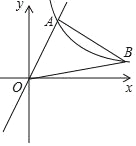
【题目】如图,在平面直角坐标系中,经过点A的双曲线y=![]() (x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为1,∠AOB=∠OBA=45°,则k的值为_____.
(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为1,∠AOB=∠OBA=45°,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
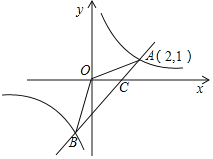
【题目】如图,一次函数y=x+m的图象与反比例函数y=![]() 的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
(1)求m及k的值;
(2)求点B的坐标及△AOB的面积;
(3)观察图象直接写出使反比例函数值小于一次函数值的自变量x取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户承包荒山种了44棵苹果树.现在进入第三年收获期.收获时,先随意摘了5棵树上的苹果,称得每棵树摘得的苹果重量如下(单位:千克)35 35 34 39 37
(1)在这个问题中,总体指的是?个体指的是?样本是?样本容量是?
(2)试根据样本平均数去估计总体情况,你认为该农户可收获苹果大约多少千克?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com