
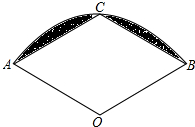
 如图,在扇形AOB中,半径OA=1,∠AOB=120°,C为弧AB的中点,连接AC、BC,则图中阴影部分的面积是
如图,在扇形AOB中,半径OA=1,∠AOB=120°,C为弧AB的中点,连接AC、BC,则图中阴影部分的面积是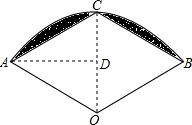 解:连接OC,过点A作AD⊥CD于点D,
解:连接OC,过点A作AD⊥CD于点D,
| ||
| 2 |
| 120π×12 |
| 360 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
| ||
| 2 |


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
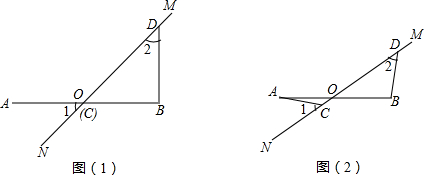
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,在等腰三角形ABC中,∠A=90°,D是斜边BC的中点,
如图所示,在等腰三角形ABC中,∠A=90°,D是斜边BC的中点,查看答案和解析>>
科目:初中数学 来源: 题型:
| A、为了了解某品牌手机的屏幕是否耐摔,选择全面调查 |
| B、为了了解玉兔号月球车的零部件质量,选择抽样调查 |
| C、为了了解南开步行街平均每天的人流量,选择抽样调查 |
| D、为了了解中秋节期间重庆市场上的月饼质量,选择全面调查 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com