
【题目】已知抛物线G:y=x2-2mx与直线l:y=3x+b相交于A,B两点(点A的横坐标小于点B的横坐标)
(1)求抛物线y=x2-2mx顶点的坐标(用含m的式子表示);
(2)已知点C(-2,1),若直线l经过抛物线G的顶点,求△ABC面积的最小值;
(3)若平移直线l,可以使A,B两点都落在x轴的下方,求实数m的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)m>3或m<-3
;(3)m>3或m<-3
【解析】
(1)将抛物线解析式化为顶点式即可求解;
(2)根据直线过抛物线顶点,可以将顶点坐标代入解析式求出b,之后联立方程求出A、B两点的坐标;过C点做CD∥y轴交直线于D,可以发现C在D的上方,并且不论CD在A、B左侧、中间还是右侧,面积的求法是一致的,即可求出面积的代数式,求出其最值即可;
(3)由(2)知B在A上方9个单位,所以只需要保证yB<0就可以了,求解不等式即可.
解:(1)∵y=x2-2mx=![]() ,
,
∴顶点为![]() ;
;
(2)∵直线过抛物线顶点,
∴![]() ,
,
即![]() ,
,
故一次函数解析式为![]() ,
,
联立方程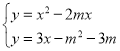 ,
,
解得 ,
,
∵点A的横坐标小于点B的横坐标,
∴将x代入解析式可求得![]() ,
,
∵C(-2,1),
∴过C点做CD∥y轴交直线于D,
则![]() ,
,
∵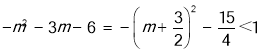 ,
,
∴![]() ,
,
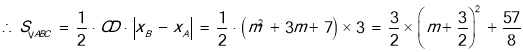 ,
,
∴△ABC面积的最小值为![]() ;
;
(3)由(2)可知![]() ,
,
故使A,B两点都落在x轴的下方只需满足![]() ,
,
解得m>3或m<-3,
∴实数m的取值范围为m>3或m<-3.


科目:初中数学 来源: 题型:
【题目】为落实疫情期间的垃圾分类,树立全面环保意识,某校举行了“垃圾分类,绿色环保”知识竞赛活动,根据学生的成绩划分为![]() ,
,![]() ,
,![]() ,
,![]() 四个等级,并绘制了不完整的两种统计图:
四个等级,并绘制了不完整的两种统计图:
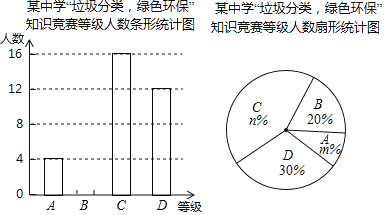
根据图中提供的信息,回答下列问题:
(1)参加知识竞赛的学生共有______人,并把条形统计图补充完整;
(2)扇形统计图中,![]() ______,
______,![]() ______,
______,![]() 等级对应的圆心角为______度;
等级对应的圆心角为______度;
(3)小明是四名获![]() 等级的学生中的一位,学校将从获
等级的学生中的一位,学校将从获![]() 等级的学生中任选取2人,参加市举办的知识竞赛,请用列表法或画树状图,求小明被选中参加区知识竞赛的概率.
等级的学生中任选取2人,参加市举办的知识竞赛,请用列表法或画树状图,求小明被选中参加区知识竞赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明对教材“课题学习”中的“用一张正方形折出一个正八边形”的问题进行了认真地探索.他先把正方形![]() 沿对角线
沿对角线![]() 对折,再把
对折,再把![]() 对折,使点
对折,使点![]() 落在
落在![]() 上,记为点
上,记为点![]() .然后沿
.然后沿![]() 的中垂线折叠,得到折痕
的中垂线折叠,得到折痕![]() ,如图1,类似地,折出其余三条折痕
,如图1,类似地,折出其余三条折痕![]() ,得到八边形
,得到八边形![]() ,如图2.
,如图2.
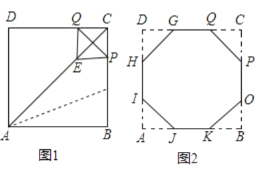
(1)求证:![]() 是等腰直角三角形.
是等腰直角三角形.
(2)若![]() ,求
,求![]() 的长.(用含
的长.(用含![]() 的代数式表示)
的代数式表示)
(3)我们把八条边长相等,八个内角都相等的八边形叫做正八边形,试说明八边形![]() 是正八边形,请把过程补充完整.
是正八边形,请把过程补充完整.
解:理由如下:
①
![]()
同理可得:![]()
②
![]()
同理可得:![]()
∴八边形![]() 是正八边形.
是正八边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD为正方形,∠CAB的角平分线交BC于点E,过点C作CF⊥AE交AE的延长线于点G,CF与AB的延长线交于点F,连接BG、DG、与AC相交于点H,则下列结论:①![]() ABE
ABE![]()
![]() CBF;②GF=CG;③BG⊥DG;④
CBF;②GF=CG;③BG⊥DG;④![]() ,其中正确的是______.
,其中正确的是______.
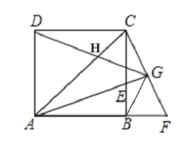
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,双曲线![]() 与直线
与直线![]() 相交于
相交于![]() ,点P是x轴上一动点.
,点P是x轴上一动点.
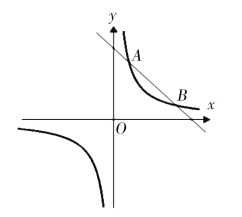
(1)求双曲线![]() 与直线
与直线![]() 的解析式;
的解析式;
(2)当![]() 时,直接写出x的取值范围;
时,直接写出x的取值范围;
(3)当![]() 是等腰三角形时,求点P的坐标.
是等腰三角形时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD//CO.

(1)求证:△ADB∽△OBC;
(2)若AB=2,BC=![]() ,求AD的长.(结果保留根号)
,求AD的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作发现:如图,已知△ABC和△ADE均为等腰三角形,AB=AC,AD=AE,将这两个三角形放置在一起,使点B,D,E在同一直线上,连接CE.

(1)如图1,若∠ABC=∠ACB=∠ADE=∠AED=55°,求证:△BAD≌△CAE;
(2)在(1)的条件下,求∠BEC的度数;
拓广探索:(3)如图2,若∠CAB=∠EAD=120°,BD=4,CF为△BCE中BE边上的高,请直接写出EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节当天,小明带了四个粽子(除味道不同外,其它均相同),其中两个是大枣味的,另外两个是火腿味的,准备按数量平均分给小红和小刚两个好朋友.
(1)请你用树状图或列表的方法表示小红拿到的两个粽子的所有可能性;
(2)请你计算小红拿到的两个粽子刚好是同一味道的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com