【题目】如图，A点的初始位置位于数轴上表示1的点，现对A点做如下移动：第1次向左移动3个单位长度至B点，第2次从B点向右移动6个单位长度至C点，第3次从C点向左移动9个单位长度至D点，第4次从D点向右移动12个单位长度至E点，…，依此类推．这样第_____次移动到的点到原点的距离为2018．
【答案】1345
【解析】
根据数轴上点的坐标变化和平移规律（左减右加），分别求出点所对应的数，进而求出点到原点的距离；然后对奇数项、偶数项分别探究，找出其中的规律（相邻两数都相差3），写出表达式就可解决问题．
第1次点A向左移动3个单位长度至点B，则B表示的数，1﹣3=﹣2；
第 2次从点B向右移动6个单位长度至点C，则C表示的数为﹣2+6=4；
第 3次从点C向左移动9个单位长度至点D，则D表示的数为4﹣9=﹣5；
第 4次从点D向右移动12个单位长度至点E，则点E表示的数为﹣5+12=7；
第 5次从点E向左移动15个单位长度至点F，则F表示的数为7﹣15=﹣8；
…；
由以上数据可知，当移动次数为奇数时，点在数轴上所表示的数满足：﹣
（3n+1），当移动次数为偶数时，点在数轴上所表示的数满足：3n﹣2．
故当移动次数为奇数时，﹣（3n+1）=﹣2018，解得：n=1345，
当移动次数为偶数时，3n﹣2=2018，n=
（不合题意）．
故答案为：1345．
一线名师权威作业本系列答案科目：初中数学 来源： 题型：
【题目】一项工程，甲，乙两公司合做，12天可以完成，共需付施工费102000元；如果甲，乙两公司单独完成此项工程，乙公司所用时间是甲公司的1.5倍，乙公司每天的施工费比甲公司每天的施工费少1500元．
（1）甲，乙两公司单独完成此项工程，各需多少天？
（2）若让一个公司单独完成这项工程，哪个公司的施工费较少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，点E在边CD上，将该矩形沿AE折叠，使点D落在边BC上的点F处，过点F作FG∥CD，交AE于点G，连接DG．
（1）求证：四边形DEFG为菱形；
（2）若CD=8，CF=4，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，
垂直平分线段
（
），点
是线段 延长线上的一点，且
，连接
，过点
作
于点
，交
的延长线与点
.
（1）若
，则
______（用
的代数式表示）；
（2）线段与线段
相等吗？为什么？
（3）若
，求
的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AB∥CD，现将一直角三角形PMN放入图中，其中∠P=90°，PM交AB于点E，PN交CD于点F
（1）当△PMN所放位置如图①所示时，则∠PFD与∠AEM的数量关系为 ；
（2）当△PMN所放位置如图②所示时，求证：∠PFD﹣∠AEM=90°；
（3）在（2）的条件下，若MN与CD交于点O，且∠DON=30°，∠PEB=15°，求∠N的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将正整数1至2019按照一定规律排成下表：
记aij表示第i行第j个数，如a14＝4表示第1行第4个数是4．
（1）直接写出a42＝ ，a53＝ ；
（2）①如果aij＝2019，那么i＝ ，j＝ ；②用i，j表示aij＝ ；
（3）将表格中的5个阴影格子看成一个整体并平移，所覆盖的5个数之和能否等于2027．若能，求出这5个数中的最小数，若不能说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法正确的个数是( )
①若某数的相反数的绝对值与其绝对值的相反数相等，则此数为零；
②若a≠0，b≠0，则a+b≠0；
③一个有理数的绝对值一定大于这个数；
④近似数2.030有4个有效数字，它们分别是2，0，3，0；
⑤若2.009
≈4.036，则2009≈4036000；
⑥当a≠1时，|a-1|与|1-a|的差没有倒数.
A. 3个B. 4个C. 5个D. 6个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，
，
点为
轴上一动点，
.
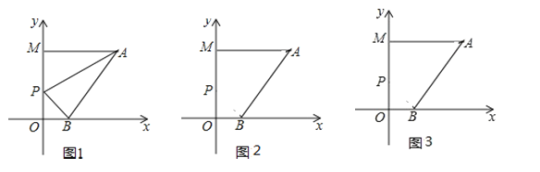
（1）求点
的坐标；
（2）不论点运动到直线
上的任何位置（不包括点
），
三者之间是否都存在某种固定的数量关系，如果有，请利用所学知识找出并证明，如果没有，请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
