
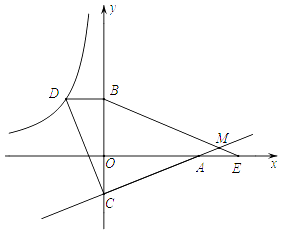
【题目】如图,已知点D在反比例函数y= ![]() 的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC= ![]() .
.
(1)求反比例函数y= ![]() 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.
【答案】
(1)
解:∵A(5,0),
∴OA=5.
∵ ![]() ,
,
∴ ![]() ,解得OC=2,
,解得OC=2,
∴C(0,﹣2),
∴BD=OC=2,
∵B(0,3),BD∥x轴,
∴D(﹣2,3),
∴m=﹣2×3=﹣6,
∴ ![]() ,
,
设直线AC关系式为y=kx+b,
∵过A(5,0),C(0,﹣2),
∴ ![]() ,解得
,解得 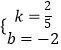 ,
,
∴ ![]()
(2)
解:∵B(0,3),C(0,﹣2),
∴BC=5=OA,
在△OAC和△BCD中

∴△OAC≌△BCD(SAS),
∴AC=CD,
∴∠OAC=∠BCD,
∴∠BCD+∠BCA=∠OAC+∠BCA=90°,
∴AC⊥CD
(3)
解:∠BMC=45°.
如图,连接AD,
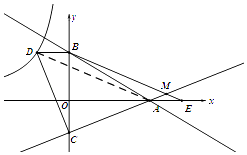
∵AE=OC,BD=OC,AE=BD,
∴BD∥x轴,
∴四边形AEBD为平行四边形,
∴AD∥BM,
∴∠BMC=∠DAC,
∵△OAC≌△BCD,
∴AC=CD,
∵AC⊥CD,
∴△ACD为等腰直角三角形,
∴∠BMC=∠DAC=45°
【解析】(1)由A点坐标可求得OA的长,再利用三角函数的定义可求得OC的长,可求得C、D点坐标,再利用待定系数法可求得直线AC的解析式;(2)由条件可证明△OAC≌△BCD,再由角的和差可求得∠OAC+∠BCA=90°,可证得AC⊥CD;(3)连接AD,可证得四边形AEBD为平行四边形,可得出△ACD为等腰直角三角形,则可求得答案.


科目:初中数学 来源: 题型:
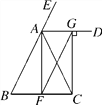
【题目】如图,∠CAE是△ABC的外角,AD平分∠EAC,且AD∥BC.过点C作CG⊥AD,垂足为G,AF是BC边上的中线,连接FG.
(1)求证:AC=FG;
(2)当AC⊥FG时,△ABC应是怎样的三角形?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠BAD的平分线与∠ADC的平分线相交于点E,∠ABC的平分线与∠BCD的平分线相交于点F,则∠E与∠F的数量关系是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车沿公路左右行驶,向左为正,向右为负,某天从A地出发后到收工回家所走的路线如下:![]() 单位:千米
单位:千米![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() 问收工时离出发点A多少千米?
问收工时离出发点A多少千米?
![]() 若该出租车每千米耗油
若该出租车每千米耗油![]() 升,问从A地出发到收工共耗油多少升?
升,问从A地出发到收工共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种商品的标准价格是200元,但随着季节的变化,商品的价格可浮动![]() ,想一想.
,想一想.
![]() 的含义是什么?
的含义是什么?
![]() 请你计算出该商品的最高价格和最低价格;
请你计算出该商品的最高价格和最低价格;
![]() 如果以标准价为标准,超过标准价记“
如果以标准价为标准,超过标准价记“![]() ”,低于标准价记“
”,低于标准价记“![]() ”,该商品价格的浮动范围又可以怎样表示?
”,该商品价格的浮动范围又可以怎样表示?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F分别在BC,CD上,△AEF是等边三角形,连接AC交EF于点G,下列结论:①CE=CF,②∠AEB=75°,③AG=2GC,④BE+DF=EF,⑤S△CEF=2S△ABE , 其中结论正确的个数为( )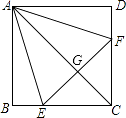
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y= ![]() 过点A(2,4),B(0,3)、题目中的矩形部分是一段因墨水污染而无法辨认的文字.
过点A(2,4),B(0,3)、题目中的矩形部分是一段因墨水污染而无法辨认的文字.
(1)根据现有的信息,请求出题中的一次函数的解析式.
(2)根据关系式画出这个函数图象.
(3)过点B能不能画出一直线BC将△ABO(O为坐标原点)分成面积比为1:2的两部分?如能,可以画出几条,并求出其中一条直线所对应的函数关系式,其它的直接写出函数关系式;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我们所学的课本中,多项式与多项式相乘可以用几何图形的面积来表示.例如,(2a+b)(a+b)=2a2+3ab+b2就可以用图(1)来表示.请你根据此方法写出图(2)中图形的面积所表示的代数恒等式:____________.

【答案】(a+2b)(2a+b)=2a2+5ab+2b2
【解析】试题分析:图②的面积可以用长为a+a+b,宽为b+a+b的长方形面积求出,也可以由四个正方形与5个小长方形的面积之和求出,表示出即可.
解:根据图形列得:(a+2b)(2a+b)=2a2+5ab+2b2.
故答案为:(a+2b)(2a+b)=2a2+5ab+2b2.
考点:多项式乘多项式.
点评:此题考查了多项式乘以多项式法则,熟练掌握法则是解本题的关键.
【题型】填空题
【结束】
18
【题目】若一个正整数能表示为两个正整数的平方差,则称这个正整数为“智慧数”(如3=22-12,16=52-32,则3和16是智慧数).已知按从小到大的顺序构成如下数列:3,5,7,8,9,11,12,13,15,16,17,19,20,21,23,24,25,…则第2 013个“智慧数”是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了切实关注、关爱贫困家庭学生,某校对全校各班贫困家庭学生的人数情况进行了统计,以便国家精准扶贫政策有效落实.统计发现班上贫困家庭学生人数分别有2名、3名、4名、5名、6名,共五种情况.并将其制成了如下两幅不完整的统计图: 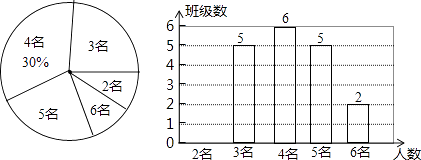
(1)求该校一共有多少个班?并将条形图补充完整;
(2)某爱心人士决定从2名贫困家庭学生的这些班级中,任选两名进行帮扶,请用列表法或树状图的方法,求出被选中的两名学生来自同一班级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com