
【题目】如图,在平面直角坐标系中,A、B两点的坐标分别为(﹣2,2)、(1,8).

(1)求三角形ABO的面积;
(2)若y轴上有一点M,且三角形MAB的面积为10,求M点的坐标;
(3)如图,把直线AB以每秒2个单位的速度向右平移,问经过多少秒后,该直线与y轴交于点(0,﹣2)?
【答案】(1)S△AOB=9;(2)M(0,![]() )或(0,﹣
)或(0,﹣![]() );(3)经过2.5秒后,该直线与y轴交于点(0,﹣2).
);(3)经过2.5秒后,该直线与y轴交于点(0,﹣2).
【解析】
(1)根据待定系数法求得直线AB的解析式,即可求得直线AB与y轴的交点D为(0,6),然后根据S△AOB=S△AOD+S△BOD求得即可;
(2)设M(0,m),则MD=|m6|,根据S△MAB=S△MAD+S△MBD=10,求得m的值,即可求得M的坐标;
(3)根据平行直线的解析式的k值相等设出平移后直线AB的解析式为y=2(x2t)+6,然后把点点(0,2)代入求出t,即可得解.
(1)设直线AB的解析式为y=kx+b,
把A(﹣2,2)、B(1,8)代入得:![]() ,
,
解得![]() ,
,
∴直线AB的解析式为y=2x+6,
∴直线AB与y轴的交点D为(0,6),
∴S△AOB=S△AOD+S△BOD=![]() ×6×2+
×6×2+![]() ×6×1=9;
×6×1=9;
(2)设M(0,m),
∴MD=|m﹣6|,
∵S△MAB=S△MAD+S△MBD=10,
∴![]() ×|m﹣6|×(2+1)=10,
×|m﹣6|×(2+1)=10,
∴m=![]() 或m=﹣
或m=﹣![]() ,
,
∴M(0,![]() )或(0,﹣
)或(0,﹣![]() );
);
(3)设经过t秒后,该直线与y轴交于点(0,﹣2),
则平移后的解析式为y=2(x﹣2t)+6,
∴﹣2=2(0﹣2t)+6,
解得t=2.5,
故经过2.5秒后,该直线与y轴交于点(0,﹣2).


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④![]() <a<
<a<![]() ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )

A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=25°,点M、N分别是边OA、OB上的定点,点P、Q分别是边OB、OA上的动点,记∠MPQ=α,∠PQN=β,当MP+PQ+QN最小时,则β﹣α的值为( )
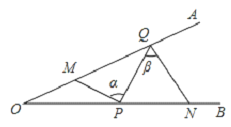
A.50°B.40°C.30°D.25°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形△ABC中,AB=3,BC=4,AC=5
(1)在图①中画一直线将△ABC分割成两个等腰三角形;
(2)现有一点P与Q在△ABC的边上运动,请在备用图上画出△APQ有一边为2的等腰三角形的四种情况.
要求:1、用有刻度的直尺简单作图,并在所画等腰三角形中边长为2的边上标注数字2即可,2即为线段BC长度的一半;2、形状一样的算一种图形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将证明过程补充完整.
如图,DE∥AB,FG⊥AC,∠1=∠3,求证:BD⊥AC.
证明:∵DE∥AB(已知),
∴∠1=_______(_______)
∵∠1=∠3(已知),
∴∠3=_______(等量代换),
∴FG∥BD(_______),
∴∠ADB=∠AFG(_______)
∵FG⊥AC(已知),
∴∠AFG=90°(垂直的定义),
∴∠ADB=90°(_______),
∴BD⊥AC(_______)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与坐标轴分别交于A,B两点,抛物线
与坐标轴分别交于A,B两点,抛物线![]() 经过点A,B,点P从点B出发,以每秒2个单位长度的速度沿射线BA运动,点Q从点A出发,以每秒1个单位长度的速度沿射线AO运动,两点同时出发,运动时间为t秒.
经过点A,B,点P从点B出发,以每秒2个单位长度的速度沿射线BA运动,点Q从点A出发,以每秒1个单位长度的速度沿射线AO运动,两点同时出发,运动时间为t秒.
![]() 求此抛物线的表达式;
求此抛物线的表达式;
![]() 求当
求当![]() 为等腰三角形时,所有满足条件的t的值;
为等腰三角形时,所有满足条件的t的值;
![]() 点P在线段AB上运动,请直接写出t为何值时,
点P在线段AB上运动,请直接写出t为何值时,![]() 的面积达到最大?此时,在抛物线上是否存在一点T,使得
的面积达到最大?此时,在抛物线上是否存在一点T,使得![]() ≌
≌![]() ?若存在,请直接写出点T的坐标;若不存在,请说明理由.
?若存在,请直接写出点T的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com