
����Ŀ����ͼ��һ�κ���![]() ��������ֱ���A��B���㣬������
��������ֱ���A��B���㣬������![]() ������A��B����P�ӵ�B��������ÿ��2����λ���ȵ��ٶ�������BA�˶�����Q�ӵ�A��������ÿ��1����λ���ȵ��ٶ�������AO�˶�������ͬʱ�������˶�ʱ��Ϊt�룮
������A��B����P�ӵ�B��������ÿ��2����λ���ȵ��ٶ�������BA�˶�����Q�ӵ�A��������ÿ��1����λ���ȵ��ٶ�������AO�˶�������ͬʱ�������˶�ʱ��Ϊt�룮
![]() ��������ߵı���ʽ��
��������ߵı���ʽ��
![]() ��
��![]() Ϊ����������ʱ����������������t��ֵ��
Ϊ����������ʱ����������������t��ֵ��
![]() ��P���߶�AB���˶�����ֱ��д��tΪ��ֵʱ��
��P���߶�AB���˶�����ֱ��д��tΪ��ֵʱ��![]() ������ﵽ���ʱ�������������Ƿ����һ��T��ʹ��
������ﵽ���ʱ�������������Ƿ����һ��T��ʹ��![]() ��
��![]() �������ڣ���ֱ��д����T�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ���ֱ��д����T�����ꣻ�������ڣ���˵�����ɣ�

���𰸡�(1)![]() ����2����
����2����![]() Ϊ����������ʱ��t��ֵΪ
Ϊ����������ʱ��t��ֵΪ![]() ��
��![]() ��
��![]() ��4����3����T������Ϊ
��4����3����T������Ϊ![]() ��
��
��������
��1������õ�A�͵�B�����꣬Ȼ��ѵ�A�͵�B������ΰ��������ߵĽ���ʽ�����b��c��ֵ���Ӷ��ɵõ������ߵĽ���ʽ��
��2���˶�t���AQ=t��BP=2t�������AB�ij���Ȼ���ΪQA=QP��AP=AQ��PA=PQ�����������⼴�ɣ�
��3������P��PF��AO�ڵ�F���ӳ�FP�����������T����AP=4-2t��PF=![]() AP=2-t��Ȼ��ɵõ�S��APQ��t�ĺ�����ϵʽ���Ӷ������t��ֵ�����ǿɵõ���P�����꣬�Ӷ�����õ�T�����꣬Ȼ����֤�����APT�ա�APO���ɣ�
AP=2-t��Ȼ��ɵõ�S��APQ��t�ĺ�����ϵʽ���Ӷ������t��ֵ�����ǿɵõ���P�����꣬�Ӷ�����õ�T�����꣬Ȼ����֤�����APT�ա�APO���ɣ�
![]() ��
��![]() ����
����![]() ����
����![]() ��
��
��![]() ����
����![]() ����
����![]() ��
��
![]() ��
��![]()
��![]() ��
��![]() �ֱ����
�ֱ����![]() �У���
����![]() ��
��![]() ��
��
�����ߵı���ʽΪ![]()
![]() ��
��![]() ���ɹ��ɶ�������
���ɹ��ɶ�������![]() ��
��
![]() ��
��
�˶�t���![]() ��
��![]() ��
��
![]() ������������
������������![]() ��
��![]() ��
��![]() ���������
���������
![]() ��
��![]() ʱ������Q��
ʱ������Q��![]() �ڵ�D��
�ڵ�D��

��![]() ��
��![]() ��
��![]()
![]() ��
��
![]() ��
��
���![]() ��
��
![]() ��
��![]() ʱ��
ʱ��
![]() ����P��x���Ϸ���ֱ��AB�ϣ�
����P��x���Ϸ���ֱ��AB�ϣ�![]() ��
��![]() ��
��
![]() ��
��![]()
���![]() ��
��
![]() ����P��x���·���ֱ��AB�ϣ�
����P��x���·���ֱ��AB�ϣ�
![]() ��
��
![]() ��
��
��ã�![]() ��
��
![]() ��
��![]() ʱ������P��
ʱ������P��![]() �ڵ�E��
�ڵ�E��

��![]() ����
����![]() ��
�У�![]()
![]()
![]() ��
��
![]() ��
��
��ã�![]()
������������![]() Ϊ����������ʱ��t��ֵΪ
Ϊ����������ʱ��t��ֵΪ![]() ��
��![]() ��
��![]() ��4��
��4��
![]() ����P��
����P��![]() �ڵ�F���ӳ�FP�����������T��
�ڵ�F���ӳ�FP�����������T��

![]() Ϊ
Ϊ![]() �ױ�AQ�ϵĸߣ�
�ױ�AQ�ϵĸߣ�
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ʱ��
ʱ��![]() ��������
��������![]() ��ʱ��PΪAB���е㣬��
��ʱ��PΪAB���е㣬��![]() ��
��
����OP����![]() ��
��
![]() ��
��![]() ��
��
![]() ��T�ĺ�����Ϊ
��T�ĺ�����Ϊ![]() ��
��
��![]() ���������ߵĽ���ʽ�ã�
���������ߵĽ���ʽ�ã�![]() ��
��
![]() ��
��
��![]() �У��ɹ��ɶ�����֪��
�У��ɹ��ɶ�����֪��![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��T������Ϊ
��T������Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ֵ����֪x��y���㣺x2+y2��4x+6y+13��0�������ʽ[��3x��y��2��4��2x+y����x��y������x��3y����x+3y��]�£���![]() y����ֵ��
y����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A��B���������ֱ�Ϊ����2��2������1��8����

��1����������ABO�������
��2����y������һ��M����������MAB�����Ϊ10����M������ꣻ
��3����ͼ����ֱ��AB��ÿ��2����λ���ٶ�����ƽ�ƣ��ʾ����������ֱ����y�ύ�ڵ㣨0����2����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ����������Ĺ�·�Ϸֱ���A��B������վ��Ҫ����������·֮���S��������һ�����˲ֿ⣬ʹ����������·�ľ�����ȣ�����Ҫ��������վ�ľ�����ȣ�������ͼ�л���������˲ֿ�P��λ��.����д��֪��������������ֻ������ͼ�ۼ���

��2����ͼ���������������У�A��B��C���ڸ���ϣ���������ƽ��ֱ������ϵ�н���������⣺

�ٷֱ�д��B��C��������꣬����B����![]() ��ԳƵĵ�B���͵�C����
��ԳƵĵ�B���͵�C����![]() ��ԳƵĵ�C�������ꣻ
��ԳƵĵ�C�������ꣻ
����ͼ�л���һ����A��B��C��DΪ������ı��Σ�ʹ��Ϊ��Գ�ͼ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�����ڵ�һ����x�ᡢy�����ƶ����ڵ�һ���ӣ�����ԭ���ƶ�����(1��0)��Ȼ����ͼ�м�ͷ��ʾ�����ƶ�����(0��0)��(1��0)��(1��1)��)(0��1)��(0��2)����������ÿ���ƶ�һ����λ����ô��2018��ʱ��������λ�õ�������( ).

A. (6��44)B. (38��44)C. (44��38)D. (44��6)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ�˷ḻѧ������������������������Ż��Ŀ��![]() ��ѧ��
��ѧ��![]() ������
������![]() ������
������![]() �ƴ��磬Ϊ�˽�ѧ����ϲ����һ�����Ż��Ŀ�������ȡ�˲���ѧ�����е��飬����������������������������ͳ��ͼ������ͼ
�ƴ��磬Ϊ�˽�ѧ����ϲ����һ�����Ż��Ŀ�������ȡ�˲���ѧ�����е��飬����������������������������ͳ��ͼ������ͼ![]() ��A��ռ���ε�Բ�Ľ�Ϊ
��A��ռ���ε�Բ�Ľ�Ϊ![]() ��ش��������⣺
��ش��������⣺

![]() ��α������ѧ������______�ˣ�
��α������ѧ������______�ˣ�
![]() ���㽫����ͳ��ͼ
���㽫����ͳ��ͼ![]() ����������
����������
![]() ��ƽʱ�Ŀƴ����У��ס��ҡ����������˱������㣬�־�����������ͬѧ����ѡ�����μӿƴ���������ǡ��ѡ�мס�����λͬѧ�ĸ���
��ƽʱ�Ŀƴ����У��ס��ҡ����������˱������㣬�־�����������ͬѧ����ѡ�����μӿƴ���������ǡ��ѡ�мס�����λͬѧ�ĸ���![]() ����״ͼ���б������
����״ͼ���б������![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,����֪����ABC��,�����²�����ͼ:�ٷֱ���B,CΪԲ��,�Դ���![]() BC�ij�Ϊ�뾶����,�����ཻ������M,N;����ֱ��MN��AB�ڵ�D,����CD.��CD=AC,��A=50��,���ACB�Ķ���Ϊ(����)
BC�ij�Ϊ�뾶����,�����ཻ������M,N;����ֱ��MN��AB�ڵ�D,����CD.��CD=AC,��A=50��,���ACB�Ķ���Ϊ(����)

A. 90��B. 95��C. 100��D. 105��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AF�ֱ���BD��CE���ڵ�G��H����1=54������2=126����
��1����֤��BD��CE��
��2����AC��CE��C����BD��B��FD��BD��D����CE��E��̽����A���F��������ϵ����֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
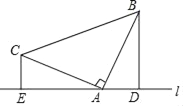
����Ŀ����֪����ͼ��ʾ����ABC�У���BAC=90�㣬AB=AC���ֱ����B��C��������A��ֱ��l�Ĵ��߶�BD��CE������ֱ�D��E��
��1����֤��DE=BD+CE��
��2���������A��ֱ�߾�����BAC���ڲ�����ô�������ۻ��������뻭��ͼ�Σ�ֱ�Ӹ�����Ľ��ۣ�����֤������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com