
ЁОЬтФПЁПЃЈ1ЃЉШчЭМЃЌСНЬѕНЛВцЕФЙЋТЗЩЯЗжБ№гаAЃЌBСНИіГЕеОЃЌвЊдкетСНЬѕЙЋТЗжЎМфЕФSЧјгђФкаовЛИіЛѕдЫВжПтЃЌЪЙЫќЕНСНЬѕЙЋТЗЕФОрРыЯрЕШЃЌЧвгжвЊЕНСНИіГЕеОЕФОрРыЯрЕШЃЌЧыФудкЭМжаЛГіетИіЛѕдЫВжПтPЕФЮЛжУ.ЃЈВЛаДвбжЊЁЂЧѓзїЁЂзїЗЈЃЌжЛБЃСєзїЭМКлМЃЃЉ

ЃЈ2ЃЉШчЭМЃЌдке§ЗНаЮЭјИёжаЃЌAЃЌBЃЌCОљдкИёЕуЩЯЃЌдкЫљИјЕФЦНУцжБНЧзјБъЯЕжаНтД№ЯТСаЮЪЬтЃК

ЂйЗжБ№аДГіBЃЌCСНЕуЕФзјБъЃЌМАЕуBЙигк![]() жсЖдГЦЕФЕуBЁфКЭЕуCЙигк
жсЖдГЦЕФЕуBЁфКЭЕуCЙигк![]() жсЖдГЦЕФЕуCЁфЕФзјБъЃЛ
жсЖдГЦЕФЕуCЁфЕФзјБъЃЛ
ЂкдкЭМжаЛГівЛИівдAЃЌBЃЌCЃЌDЮЊЖЅЕуЕФЫФБпаЮЃЌЪЙЦфЮЊжсЖдГЦЭМаЮ.
ЁОД№АИЁПЃЈ1ЃЉД№АИМћНтЮіЃЛЃЈ2ЃЉЂйBЃЈЉ1ЃЌ1ЃЉЃЌCЃЈ3ЃЌ1ЃЉЃЌBЁфЃЈЉ1ЃЌЉ1ЃЉЃЌCЁфЃЈЉ3ЃЌ1ЃЉЃЛ
ЂкД№АИМћНтЮіЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШзїГіABЕФДЙжБЦНЗжЯпЃЌШЛКѓдйзїГіl1КЭl2ЕФМаНЧНЧЦНЗжЯпЃЌСНЯпЕФНЛЕуОЭЪЧPЕФЮЛжУЃЎ
ЃЈ2ЃЉЂйИљОнЙигкxжсЁЂyжсЖдГЦЕФЕуЕФКсзнзјБъЕФЙиЯЕПЩЕУНсТлЃЛ
ЂкИљОнжсЖдГЦЕФЖЈвхзїЭММДПЩЃЎ
ЃЈ1ЃЉШчЭМЫљЪОЃК
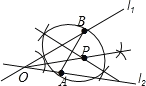
ЕуPМДЮЊЫљЧѓЃЎ
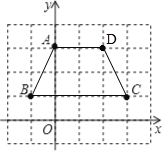
ЃЈ2ЃЉЂйгЩЭМПЩжЊЃКBЃЈЉ1ЃЌ1ЃЉЃЌCЃЈ3ЃЌ1ЃЉЃЎЕуBЃЈЉ1ЃЌ1ЃЉЙигкxжсЕФЖдГЦЕуBЁфЕФзјБъЮЊЃЈЉ1ЃЌЉ1ЃЉЃЌЕуCЃЈ3ЃЌ1ЃЉЙигкyжсЕФЖдГЦЕуCЁфЕФзјБъЃЈЉ3ЃЌ1ЃЉЃЛ
ЂкШчЭМЫљЪОЃЌЫФБпаЮABCDМДЮЊжсЖдГЦЭМаЮЃЎ


 аЁбЇЩњ10ЗжжгПкЫуВтЪд100ЗжЯЕСаД№АИ
аЁбЇЩњ10ЗжжгПкЫуВтЪд100ЗжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФЗНГЬx2+2(a+1)x+(3a2+4ab+4b2+2)ЃН0гаЪЕИљЃЌдђaЁЂbЕФжЕЗжБ№ЮЊ______________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкАыОЖЮЊ2cmЃЌдВаФНЧЮЊ90ЁуЕФЩШаЮOABжаЃЌЗжБ№вдOAЁЂOBЮЊжБОЖзїАыдВЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧШ§НЧаЮЁїABCжаЃЌABЃН3ЃЌBCЃН4ЃЌACЃН5
ЃЈ1ЃЉдкЭМЂйжаЛвЛжБЯпНЋЁїABCЗжИюГЩСНИіЕШбќШ§НЧаЮЃЛ
ЃЈ2ЃЉЯжгавЛЕуPгыQдкЁїABCЕФБпЩЯдЫЖЏЃЌЧыдкБИгУЭМЩЯЛГіЁїAPQгавЛБпЮЊ2ЕФЕШбќШ§НЧаЮЕФЫФжжЧщПіЃЎ
вЊЧѓЃК1ЁЂгУгаПЬЖШЕФжБГпМђЕЅзїЭМЃЌВЂдкЫљЛЕШбќШ§НЧаЮжаБпГЄЮЊ2ЕФБпЩЯБъзЂЪ§зж2МДПЩЃЌ2МДЮЊЯпЖЮBCГЄЖШЕФвЛАыЃЛ2ЁЂаЮзДвЛбљЕФЫувЛжжЭМаЮЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋжЄУїЙ§ГЬВЙГфЭъећЃЎ
ШчЭМЃЌDEЁЮABЃЌFGЁЭACЃЌЁЯ1=ЁЯ3ЃЌЧѓжЄЃКBDЁЭACЃЎ
жЄУїЃКЁпDEЁЮAB(вбжЊ)ЃЌ
ЁрЁЯ1=_______(_______)
ЁпЁЯ1=ЁЯ3(вбжЊ)ЃЌ
ЁрЁЯ3=_______(ЕШСПДњЛЛ)ЃЌ
ЁрFGЁЮBD(_______)ЃЌ
ЁрЁЯADB=ЁЯAFG(_______)
ЁпFGЁЭAC(вбжЊ)ЃЌ
ЁрЁЯAFG=90Ёу(ДЙжБЕФЖЈвх)ЃЌ
ЁрЁЯADB=90Ёу(_______)ЃЌ
ЁрBDЁЭAC(_______)

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дквбжЊЕФЁїABCжа,АДвдЯТВНжшзїЭМ:ЂйЗжБ№вдB,CЮЊдВаФ,вдДѓгк![]() BCЕФГЄЮЊАыОЖзїЛЁ,СНЛЁЯрНЛгкСНЕуM,N;ЂкзїжБЯпMNНЛABгкЕуD,СЌНгCD.ШєCD=AC,ЁЯA=50Ёу,дђЁЯACBЕФЖШЪ§ЮЊ(ЁЁЁЁ)
BCЕФГЄЮЊАыОЖзїЛЁ,СНЛЁЯрНЛгкСНЕуM,N;ЂкзїжБЯпMNНЛABгкЕуD,СЌНгCD.ШєCD=AC,ЁЯA=50Ёу,дђЁЯACBЕФЖШЪ§ЮЊ(ЁЁЁЁ)

A. 90ЁуB. 95ЁуC. 100ЁуD. 105Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§![]() гызјБъжсЗжБ№НЛгкAЃЌBСНЕуЃЌХзЮяЯп
гызјБъжсЗжБ№НЛгкAЃЌBСНЕуЃЌХзЮяЯп![]() ОЙ§ЕуAЃЌBЃЌЕуPДгЕуBГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбиЩфЯпBAдЫЖЏЃЌЕуQДгЕуAГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШбиЩфЯпAOдЫЖЏЃЌСНЕуЭЌЪБГіЗЂЃЌдЫЖЏЪБМфЮЊtУыЃЎ
ОЙ§ЕуAЃЌBЃЌЕуPДгЕуBГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбиЩфЯпBAдЫЖЏЃЌЕуQДгЕуAГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШбиЩфЯпAOдЫЖЏЃЌСНЕуЭЌЪБГіЗЂЃЌдЫЖЏЪБМфЮЊtУыЃЎ
![]() ЧѓДЫХзЮяЯпЕФБэДяЪНЃЛ
ЧѓДЫХзЮяЯпЕФБэДяЪНЃЛ
![]() ЧѓЕБ
ЧѓЕБ![]() ЮЊЕШбќШ§НЧаЮЪБЃЌЫљгаТњзуЬѕМўЕФtЕФжЕЃЛ
ЮЊЕШбќШ§НЧаЮЪБЃЌЫљгаТњзуЬѕМўЕФtЕФжЕЃЛ
![]() ЕуPдкЯпЖЮABЩЯдЫЖЏЃЌЧыжБНгаДГіtЮЊКЮжЕЪБЃЌ
ЕуPдкЯпЖЮABЩЯдЫЖЏЃЌЧыжБНгаДГіtЮЊКЮжЕЪБЃЌ![]() ЕФУцЛ§ДяЕНзюДѓЃПДЫЪБЃЌдкХзЮяЯпЩЯЪЧЗёДцдквЛЕуTЃЌЪЙЕУ
ЕФУцЛ§ДяЕНзюДѓЃПДЫЪБЃЌдкХзЮяЯпЩЯЪЧЗёДцдквЛЕуTЃЌЪЙЕУ![]() Ёе
Ёе![]() ЃПШєДцдкЃЌЧыжБНгаДГіЕуTЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃПШєДцдкЃЌЧыжБНгаДГіЕуTЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФБпГЄЮЊ4ЃЌOЪЧADЕФжаЕуЃЌЖЏЕуEдкЯпЖЮABЩЯЃЌСЌНгEOВЂбгГЄНЛЩфЯпCDгкЕуFЃЌЙ§OзїEFЕФДЙЯпНЛЩфЯпBCгкЕуGЃЌСЌНгEGЁЂFGЃЎ
![]() ШчЭМ1ЃЌХаЖЯ
ШчЭМ1ЃЌХаЖЯ![]() ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
![]() ШчЭМ1ЃЌЩш
ШчЭМ1ЃЌЩш![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊyЃЌЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЕФУцЛ§ЮЊyЃЌЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЛ
![]() НЋЕуAбижБЯпEOЗелЃЌЕУЕНЕу
НЋЕуAбижБЯпEOЗелЃЌЕУЕНЕу![]() ШчЭМ2ЃЌЧыМЦЫудкЕуEдЫЖЏЕФЙ§ГЬжаЃЌЕуGдЫЖЏТЗОЖЕФГЄЖШ
ШчЭМ2ЃЌЧыМЦЫудкЕуEдЫЖЏЕФЙ§ГЬжаЃЌЕуGдЫЖЏТЗОЖЕФГЄЖШ![]() ВЂЗжБ№ЧѓГіЕБЕуGЮЛгкТЗОЖЕФЦ№ЕуКЭжеЕуЪБЃЌ
ВЂЗжБ№ЧѓГіЕБЕуGЮЛгкТЗОЖЕФЦ№ЕуКЭжеЕуЪБЃЌ![]() ЕФжЕЃП
ЕФжЕЃП




ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌвбжЊЕуDдкЯпЖЮABЕФЗДЯђбгГЄЯпЩЯЃЌЙ§ACЕФжаЕуFзїЯпЖЮGEНЛЁЯDACЕФЦНЗжЯпгкEЃЌНЛBCгкGЃЌЧвAEЁЮBCЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїABCЪЧЕШбќШ§НЧаЮЃЛ
ЃЈ2ЃЉШєAEЃН8ЃЌABЃН10ЃЌGCЃН2BGЃЌЧѓЁїABCЕФжмГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com