
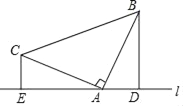
【题目】已知:如图所示,△ABC中,∠BAC=90°,AB=AC,分别过点B、C作经过点A的直线l的垂线段BD、CE,垂足分别D、E.
(1)求证:DE=BD+CE.
(2)如果过点A的直线经过∠BAC的内部,那么上述结论还成立吗?请画出图形,直接给出你的结论(不用证明).
【答案】(1)见解析;(2)上述结论不成立.
【解析】试题分析:(1)由垂线的定义和角的互余关系得出![]()
![]() 由AAS证明
由AAS证明![]() ≌
≌![]() ,得出对应边相等
,得出对应边相等![]() 由
由![]() 即可得出结论;
即可得出结论;
(2)由垂线的定义和角的互余关系得出![]() 由AAS证明
由AAS证明![]() ≌
≌![]() ,得出对应边相等
,得出对应边相等![]() 由
由![]() 之间的和差关系,即可得出结论.
之间的和差关系,即可得出结论.
试题解析:(1)∵∠BAC=![]() ,
,
∴∠BAD+∠CAE=![]() ,
,
∵BD⊥l,CE⊥l,
∴∠ADB=∠CEA=![]() ,
,
∴∠BAD+∠ABD=![]() ,
,
∴∠ABD=∠CAE.
在△ABD和△CAE中,

∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AD+AE=DE,
∴BD+CE=DE;
(2)上述结论不成立,
如图所示,BD=DE+CE.
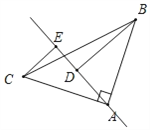
证明:∵∠BAC=![]() ,
,
∴∠BAD+∠CAE=![]() ,
,
∵BD⊥l,CE⊥l,
∴∠ADB=∠CEA=![]() ,
,
∴∠BAD+∠ABD=![]() ,
,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AD+DE=AE,
∴BD=DE+CE.
如图所示,CE=DE+BD,
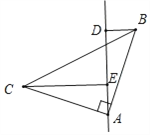
证明:证明:∵∠BAC=![]() ,
,
∴∠BAD+∠CAE=![]() ,
,
∵BD⊥l,CE⊥l,
∴∠ADB=∠CEA=![]() ,
,
∴∠BAD+∠ABD=![]() ,
,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
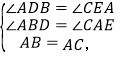
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AE+DE=AD,
∴CE=DE+BD.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两家商场进行促销活动,甲商场采用“满200减100”的促销方式,即购买商品的总金额满200元但不足400元,少付100元;满400元但不足600元,少付200元;……,乙商场按顾客购买商品的总金额打6折促销.
(1)若顾客在甲商场购买了510元的商品,付款时应付多少钱?
(2)若顾客在甲商场购买商品的总金额为x(400≤x<600)元,优惠后得到商家的优惠率为p(p=![]() ),写出p与x之间的函数关系式,并说明p随x的变化情况;
),写出p与x之间的函数关系式,并说明p随x的变化情况;
(3)品牌、质量、规格等都相同的某种商品,在甲乙两商场的标价都是x(200≤x<400)元,你认为选择哪家商场购买商品花钱较少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形的边长为2,中心为O,从O、A、B、C、D五点中任取两点.
(1)求取到的两点间的距离为2的概率;
(2)求取到的两点间的距离为![]() 的概率;
的概率;
(3)求取到的两点间的距离为![]() 的概率.
的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.

(1)已知CD=4cm,求AC的长;
(2)求证:AB=AC+CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①全等三角形的形状相同、大小相等;②全等三角形的对应边相等;③ 全等三角形的对应角相等;④全等三角形的周长相等,面积不相等,其中正确的为
( )
A. ①②③④ B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①带根号的数是无理数;②不含根号的数一定是有理数;③无理数是开方开不尽的数;④无限不循环小数是无理数;⑤π是无理数,其中正确的有( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com