
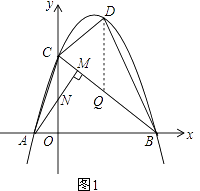
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��l��x�ᡢy��ֱ��ڵ�B��4��0����C��0��3������AΪx�Ḻ������һ�㣬AM��BC�ڵ�M��y���ڵ�N������4CN=5ON����֪������y=ax2+bx+c������A��B��C��
��1���������ߵĺ�����ϵʽ��
��2������AC����D���߶�BC�Ϸ����������ϣ�����DC��DB������BCD�͡�ABC�������S��BCD= ![]() S��ABC �� ���D�����ꣻ
S��ABC �� ���D�����ꣻ
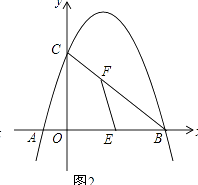
��3����ͼ2��EΪOB�е㣬��FΪ�߶�BC��һ�㣨�����˵㣩������EF��һ����P��E���������߶�EF��ÿ��1����λ���ٶ��˶���F���������߶�FC��ÿ�� ![]() ����λ���ٶ��˶���C��ֹͣ������P�������˶���������ʱ���٣���ֱ��д������ʱ��ʹ�ʱ��F�����꣮
����λ���ٶ��˶���C��ֹͣ������P�������˶���������ʱ���٣���ֱ��д������ʱ��ʹ�ʱ��F�����꣮
���𰸡�
��1��
�⣺��C��0��3����
��OC=3��
��4CN=5ON��
��ON= ![]() ��
��
�ߡ�OAN=��NCM��
���AON�ס�COB��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() �����OA=1��
�����OA=1��
��A����1��0����
�������߽���ʽΪy=a��x+1����x��4����
��C��0��3�������a1����4��=3�����a=�� ![]() ��
��
�������߽���ʽΪy=�� ![]() ��x+1����x��4��=��
��x+1����x��4��=�� ![]() x2+
x2+ ![]() x+3��
x+3��
��2��
�⣺��ֱ��BC�Ľ���ʽΪy=mx+n��
��C��0��3����B��4��0������� ![]() �����
�����  ��
��
��ֱ��BC�Ľ���ʽΪy=�� ![]() x+3��
x+3��
��PQ��y�ύBC��Q����ͼ1��
��P��x���� ![]() x2+
x2+ ![]() x+3������Q��x����
x+3������Q��x���� ![]() x+3����
x+3����
DQ=�� ![]() x2+
x2+ ![]() x+3������
x+3������ ![]() x+3��=��
x+3��=�� ![]() x2+3x��
x2+3x��
��S��BCD=S��CDQ+S��BDQ= ![]() 4����
4���� ![]() x2+3x��=��
x2+3x��=�� ![]() x2+6x��
x2+6x��
��S��BCD= ![]() S��ABC��
S��ABC��
�ੁ ![]() x2+6x=
x2+6x= ![]() ��
�� ![]() ����4+1����3��
����4+1����3��
������x2��4x+3=0�����x1=1��x2=3��
��D��������1�� ![]() ����3��3����
����3��3����
��3��
�⣺��F��m���� ![]() x+3������EF=
x+3������EF= ![]() =
= ![]() ��CF=
��CF= ![]() ��
��
��P�������˶�����������ʱ��t=EF+ ![]() =EF+
=EF+ ![]() CF��2
CF��2 ![]() ����EF=
����EF= ![]() CFʱ��ȡ�Ⱥţ���ʱt��С��
CFʱ��ȡ�Ⱥţ���ʱt��С��
�� ![]() x2��
x2�� ![]() x+13=��
x+13=�� ![]()
![]() x��2��
x��2��
������2x2��17x+26�����x1=2��x2= ![]() ����ȥ����
����ȥ����
���P�������˶����������õ�����ʱ��2�� ![]() ��2=3�룬��ʱ��F������Ϊ��2��
��2=3�룬��ʱ��F������Ϊ��2�� ![]() ����
����
����������1��������OC=3��4CN=5ON�����ON= ![]() ����֤����AON�ס�COB���������Ʊȼ����OA=1���õ�A����1��0����Ȼ�����ý���ʽ����������߽���ʽΪy=��
����֤����AON�ס�COB���������Ʊȼ����OA=1���õ�A����1��0����Ȼ�����ý���ʽ����������߽���ʽΪy=�� ![]() x2+
x2+ ![]() x+3����2�������ô���ϵ�������ֱ��BC�Ľ���ʽΪy=��
x+3����2�������ô���ϵ�������ֱ��BC�Ľ���ʽΪy=�� ![]() x+3����PQ��y�ύBC��Q����ͼ1����P��x����
x+3����PQ��y�ύBC��Q����ͼ1����P��x���� ![]() x2+
x2+ ![]() x+3������Q��x����
x+3������Q��x���� ![]() x+3�����ټ����DQ=��
x+3�����ټ����DQ=�� ![]() x2+3x�����������������ʽ��S��BCD=S��CDQ+S��BDQ=��
x2+3x�����������������ʽ��S��BCD=S��CDQ+S��BDQ=�� ![]() x2+6x��Ȼ�����S��BCD=
x2+6x��Ȼ�����S��BCD= ![]() S��ABC�õ���
S��ABC�õ��� ![]() x2+6x=
x2+6x= ![]() ��
�� ![]() ����4+1����3��Ȼ��ⷽ�����x���ɵõ�D�����ꣻ��3����F��m����
����4+1����3��Ȼ��ⷽ�����x���ɵõ�D�����ꣻ��3����F��m���� ![]() x+3�����������ľ��빫ʽ�õ�EF=
x+3�����������ľ��빫ʽ�õ�EF= ![]() ��CF=
��CF= ![]() x�����P�������˶�����������ʱ��t=EF+
x�����P�������˶�����������ʱ��t=EF+ ![]() =EF+
=EF+ ![]() CF�����ݲ���ʽ��ʽ�õ�EF+
CF�����ݲ���ʽ��ʽ�õ�EF+ ![]() CF��2
CF��2 ![]() ����EF=
����EF= ![]() CFʱ��ȡ�Ⱥţ���ʱt��С���ⷽ��
CFʱ��ȡ�Ⱥţ���ʱt��С���ⷽ�� ![]() x2��
x2�� ![]() x+13=��
x+13=�� ![]()
![]() x��2��x1=2��x2=
x��2��x1=2��x2= ![]() ����ȥ�������ǵõ���P�������˶����������õ�����ʱ��2��
����ȥ�������ǵõ���P�������˶����������õ�����ʱ��2�� ![]() ��2=3�룬��ʱ��F������Ϊ��2��
��2=3�룬��ʱ��F������Ϊ��2�� ![]() ����
����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ��κ���y=x2��3x+2��һ�κ���y=��2x+4����y=t��x2��3x+2��+��1��t������2x+4����Ϊ�����������ġ��������κ�����������t�Dz�Ϊ���ʵ������ͼ�����������E�����е�A��2��0����������E�ϵĵ�B����1��n�����������������
��1�������ԡ��ٵ�t=2ʱ��������y=t��x2��3x+2��+��1��t������2x+4���Ķ�������Ϊ
��2�����жϵ�A�Ƿ���������E�ϣ�
��3������n��ֵ��
��4�������֡�ͨ����2���ͣ�3���������֪������tȡ�κβ�Ϊ���ʵ����������E�ܹ����㣬����Ϊ ��
��5����Ӧ�á�
�ٶ��κ���y=��3x2+5x+2�Ƕ��κ���y=x2��3x+3��һ�κ���y=��2x+4��һ�����������κ�����������ǣ����t��ֵ��������ǣ�˵�����ɣ�
����ABΪ��������ABCD��ʹ������һ����������y���ϣ���������E����A��B��C��D���е����㣬������з���������t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������꼶��ʦ���Ծ���������ѧ�������������Ƚ������۵��飬��������ĿΪ�������ɡ�����˼����רע������������Ŀ��������������ȡ������������ѧ���IJ�����������Ƴ���ͼ��ʾ��Ƶ���ֲ�ֱ��ͼ������ͳ��ͼ�������������������ͼ��������Ϣ����������⣺ 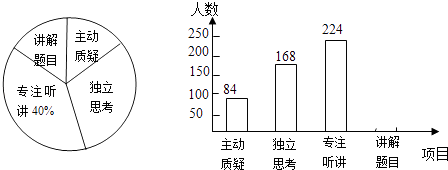
��1������������У�һ���������ѧ����
��2��������ͳ��ͼ�У���Ŀ���������ɡ����ڵ����ε�Բ�ĽǵĶ���Ϊ�ȣ�
��3���뽫Ƶ���ֲ�ֱ��ͼ����������
��4�����ȫ����6000������ѧ������ô���Ծ��������У�������˼�����ij���ѧ��Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A������E��B��C��O����C��0��8����E����6��0����O��0��0������cos��OBC��ֵΪ�� �� 
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�E��AD���ϵ��е㣬����BE�����ӳ�BE��CD���ӳ����ڵ�F�� 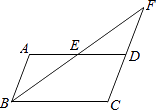
��1��֤����FD=AB��
��2����ABCD�����Ϊ8ʱ�����FED�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У���E�ڱ�DC�ϣ�DE��EC=3��1������AE��BD�ڵ�F�����DEF��������BAF�����֮��Ϊ�� �� 
A.3��4
B.9��16
C.4��9
D.1��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=ax+b��a��0����ͼ���뷴��������y= ![]() ��k��0����ͼ���ڵڶ����������ڵ�A��B���㣬��y�ύ��C�㣬����A��AH��y�ᣬ����ΪH��OH=3��tan��AOH=
��k��0����ͼ���ڵڶ����������ڵ�A��B���㣬��y�ύ��C�㣬����A��AH��y�ᣬ����ΪH��OH=3��tan��AOH= ![]() ����B������Ϊ��m����2����
����B��������m����2���� 
��1����÷�����������һ�κ����Ľ���ʽ��
��2�����AOC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���α�����һ�����⣺
��һ��������״��ͼ1���ϲ���һ����Բ���²���һ�����Σ������������IJ����ܳ�Ϊ6m�����������������ʹ��������
�������Ĵ��ǣ���������Բ�İ뾶ԼΪ0.35mʱ����������ֵԼΪ1.05m2 ��
��������ı������������״���ϲ���Ϊ��������������ɵľ��Σ���ͼ2�������ܳ���Ϊ6m������ͼ3������������⣺
��1����ABΪ1m�����ʱ�������������
��2����α��е�����Ƚϣ��ı䴰����״��������������ֵ��û�б����ͨ������˵����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y=ax+b�ͷ���������y= ![]() ��ͬһƽ��ֱ������ϵ�е�ͼ����ͼ��ʾ������κ���y=ax2+bx+c��ͼ�����Ϊ��������
��ͬһƽ��ֱ������ϵ�е�ͼ����ͼ��ʾ������κ���y=ax2+bx+c��ͼ�����Ϊ�������� 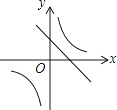
A.
B.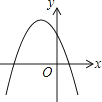
C.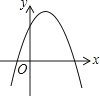
D.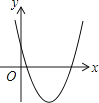
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com