
����Ŀ�����ڶ��κ���y=x2��3x+2��һ�κ���y=��2x+4����y=t��x2��3x+2��+��1��t������2x+4����Ϊ�����������ġ��������κ�����������t�Dz�Ϊ���ʵ������ͼ�����������E�����е�A��2��0����������E�ϵĵ�B����1��n�����������������
��1�������ԡ��ٵ�t=2ʱ��������y=t��x2��3x+2��+��1��t������2x+4���Ķ�������Ϊ
��2�����жϵ�A�Ƿ���������E�ϣ�
��3������n��ֵ��
��4�������֡�ͨ����2���ͣ�3���������֪������tȡ�κβ�Ϊ���ʵ����������E�ܹ����㣬����Ϊ ��
��5����Ӧ�á�
�ٶ��κ���y=��3x2+5x+2�Ƕ��κ���y=x2��3x+3��һ�κ���y=��2x+4��һ�����������κ�����������ǣ����t��ֵ��������ǣ�˵�����ɣ�
����ABΪ��������ABCD��ʹ������һ����������y���ϣ���������E����A��B��C��D���е����㣬������з���������t��ֵ��
���𰸡�
��1����1����2��
��2��
�⣺��x=2ʱ��y=t��4��6+2��+��1��t������4+4��=0��
���A��2��0����������E��
��3��
�⣺������1��n������y=t��x2��3x+2��+��1��t������2x+4����
��n=t��1+3+2��+��1��t����2+4��=6��
��n��ֵΪ6
��4��A��2��0����B����1��6��
��5��
�⣺�ٲ��ǣ�
�߽�x=��1����y=��3x2+5x+2���õ�y=��6��6��
����κ���y=y=��3x2+5x+2��ͼ������B��
����κ���y=��3x2+5x+2���Ƕ��κ���y=x2��3x+3��һ�κ���y=��2x+4��һ�����������κ�����
����ͼ��������ABC1D1�;���ABC2D2������B��BK��y����K������D1��D1G��x����G������C2��C2H��y����H������B��BM��x����M��C2H��BM���ڵ�T��

��AM=3��BM=6��BK=1��
�ɡ�KBC1�ס�MBA���� ![]() =
= ![]() ����
���� ![]() =
= ![]() �����C1K=
�����C1K= ![]() ��
��
��C1��0�� ![]() ����
����
�ɡ�KBC1�ա�GAD1���õ�AG=KB=1��GD1=KC1= ![]() ��
��
��D1��3�� ![]() ����
����
�ɡ�OAD2�ס�GAD1���õ� ![]() =
= ![]() ���ɵ�OD2=1��
���ɵ�OD2=1��
��D2��0����1����
�ɡ�TBC2�ա�OD2A���õ�TC2=OA=2��BT=OD2=1��
��C3����3��5����
�����������Ǿ���A��B��
���������������ֻ������A��B��C��A��B��D��
�ٵ������߾���A��B��C1ʱ����C1��0�� ![]() ������y=t��x2��3x+2��+��1��t������2x+4�����õ�t=��
������y=t��x2��3x+2��+��1��t������2x+4�����õ�t=�� ![]() ��
��
�ڵ������߾���A��B��D1ʱ����D1��3�� ![]() ������y=t��x2��3x+2��+��1��t������2x+4�����õ�t=
������y=t��x2��3x+2��+��1��t������2x+4�����õ�t= ![]() ��
��
�۵������߾���A��B��C2ʱ����C2����3��5������y=t��x2��3x+2��+��1��t������2x+4�����õ�t=�� ![]()
�ܵ������߾���A��B��D2ʱ����D2��0����1������y=t��x2��3x+2��+��1��t������2x+4�����õ�t= ![]() ��
��
��������������������t��ֵΪ�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]()
�������������ԡ���1���⣺��t=2ʱ��
������y=2��x2��3x+2��+��1��2������2x+4��
=2x2��4x
=2��x��1��2��2��
�ඥ�����꣨1����2����
���Դ��ǣ�1����2����
�����֡��⣺ͨ����2���ͣ�3���������֪������tȡ�κβ�Ϊ���ʵ����������E�ܹ����㣬����ΪA��2��0����B����1��6����
���Դ���A��2��0����B����1��6����
�����㾫�������ڱ��⿼��Ķ��κ�����ͼ��Ͷ��κ��������ʣ���Ҫ�˽���κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С���ܵó���ȷ�𰸣�


 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�����κ���y=ax2+bx+c��a��0����ͼ��������4�����ۣ���abc��0����b��a+c����4a+2b+c��0����b2��4ac��0��������ȷ���� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�E��AD���е㣬����CDE��CE�۵���A�͵�Dǡ���غϣ�������ABCD�����Ϊ4 ![]() ��������ABCD���ܳ��ǣ� ��
��������ABCD���ܳ��ǣ� �� 
A.8 ![]()
B.16 ![]()
C.8 ![]()
D.16 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ƽ��ֱ������ϵ�У������� ![]() ��x����A��B���㣬��y���ڵ�C���ҶԳ���Ϊx=��2����P��0��t����y���ϵ�һ�����㣮
��x����A��B���㣬��y���ڵ�C���ҶԳ���Ϊx=��2����P��0��t����y���ϵ�һ�����㣮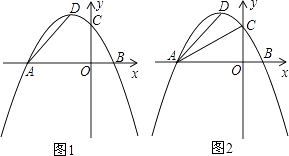
��1���������ߵĽ���ʽ������D�����꣮
��2����ͼ1����0��t��4ʱ�����PAD�����ΪS�����S��t֮��ĺ�����ϵʽ��S�Ƿ�����Сֵ������У����S����Сֵ�ʹ�ʱt��ֵ��
��3����ͼ2������P�˶���ʹ��PDA=90��ʱ��Rt��ADP��Rt��AOC�Ƿ����ƣ������ƣ������P�����ꣻ�������ƣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ʽ��M����a+5��x3+7x2��2x+5�ǹ���x�Ķ��ζ���ʽ���Ҷ�����ϵ��Ϊb��������A��B��������Ӧ�����ֱ���a��b��
��1����a���� ����b���� ����A��B����֮��ľ��룽�� ����
��2����һ����P�ӵ�A������һ�������˶�1����λ���ȣ�Ȼ�����µ�λ�õڶ����˶��������˶�2����λ���ȣ��ڴ�λ�õ������˶��������˶�3����λ���ȡ�������˹��ɲ��ϵ������˶������˶���2015��ʱ�����P����Ӧ����������
��3���ڣ�2���������£���P�����ij���˶�ʱǡ�õ���ijһλ�ã�ʹ��P����B�ľ����ǵ�P����A�ľ����3�����������������ʱ��P��λ�ã���ֱ��ָ���ǵڼ����˶�������������˵�����ɣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��������3��Ů���������ȡ�μӡ��Ұ��γǡ��ݽ�������ͬѧ��
��1������ȡ1����ǡ���������ĸ���Ϊ��
��2������ȡ2������ǡ����2��Ů���ĸ��ʣ�������״ͼ���б�����⣩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1����7��5��
��2������15��������9��
��3������5��������7��+20�£���4��
��4����![]() ��������36��
��������36��
��5����81��![]() ��
��![]() �£���16��
�£���16��
��6��5![]() ������2
������2![]() ��+����3
��+����3![]() ������+4
������+4![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ�˽���꼶ѧ��������״�����Ӱ��꼶ѧ���������ȡ����ѧ�����а˰��������ܲ��ԣ����Խ����ΪA��B��C��D�ĸ��ȼ������������ͳ��ͼ�е���Ϣ�ش��������⣺ 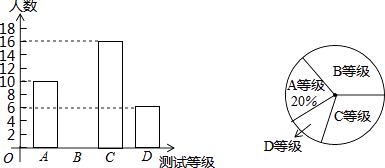
��1���β��Թ������˶�����ѧ����
��2���β��Խ��ΪB�ȼ���ѧ����������ȫ����ͳ��ͼ��
��3��������ѧ���꼶����900��ѧ����������ư��꼶ѧ�������ܲ��Խ��ΪD�ȼ���ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��l��x�ᡢy��ֱ��ڵ�B��4��0����C��0��3������AΪx�Ḻ������һ�㣬AM��BC�ڵ�M��y���ڵ�N������4CN=5ON����֪������y=ax2+bx+c������A��B��C��
��1���������ߵĺ�����ϵʽ��
��2������AC����D���߶�BC�Ϸ����������ϣ�����DC��DB������BCD�͡�ABC�������S��BCD= ![]() S��ABC �� ���D�����ꣻ
S��ABC �� ���D�����ꣻ
��3����ͼ2��EΪOB�е㣬��FΪ�߶�BC��һ�㣨�����˵㣩������EF��һ����P��E���������߶�EF��ÿ��1����λ���ٶ��˶���F���������߶�FC��ÿ�� ![]() ����λ���ٶ��˶���C��ֹͣ������P�������˶���������ʱ���٣���ֱ��д������ʱ��ʹ�ʱ��F�����꣮
����λ���ٶ��˶���C��ֹͣ������P�������˶���������ʱ���٣���ֱ��д������ʱ��ʹ�ʱ��F�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com