
ĄŸÌâÄżĄżżŐÖĐÀÂł”ÊÇÂĂÓÎʱÉÏÉœșÍœűĐĐżŐÖĐČÎč۔Ĝ»Íšč€ŸßŁŹĐĄĂśÒ»ŒÒÈ„ÄłÖűĂû·çŸ°ÇűÂĂÓÎŁŹŚŒ±žÏÈŽÓÉœœĆBŚßÌšœŚČœĐĐ”œAŁŹÔÙ»»łËÀÂł””œÉœÏDŁźŽÓB”œA”Ä·Ï߿ɿŽŚśÊÇÆÂœÇÎȘ50Ąă”ÄбÆÂŁŹł€¶ÈÎȘ3000ĂŚŁ»ŽÓA”œD”ÄÀÂł”·Ï߿ɿŽŚśÖ±ÏߣŹÓëËźÆœÏß”ÄŒĐœÇÎȘ30ĄăŁŹÇÒÀÂł”ŽÓA”œD”ÄÆœŸùËÙ¶ÈÎȘ6m/sŁŹÊ±ŒäÎȘ10·ÖÖÓŁŹÇóÉœ¶„D”Äžß¶ÈŁŹŁšČÎżŒÊęŸĘŁșsin50ĄăĄÖ0.77ŁŹcos50ĄăĄÖ0.64ŁŹtan50ĄăĄÖ1.2Ł©
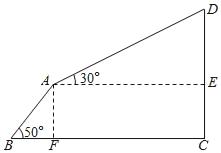
ĄŸŽđ°žĄżÉœ¶„D”Ğ߶ÈÔŒÎȘ4110ĂŚŁź
ĄŸœâÎöĄż
čęAŚśAFĄÍBCÓÚFŁŹAEĄÍCDÓÚEŁŹÔòËıßĐÎAECFÊÇŸŰĐÎŁŹÄÇĂŽCE=AFŁźœâÖ±œÇĄśABFÇółöAFŁŹœâÖ±œÇĄśDAEÇółöDEŁŹŽúÈëCD=CE+DEŁŹŒŽżÉÇółöŽđ°žŁź
ÈçÍŒŁŹčęAŚśAFĄÍBCÓÚFŁŹAEĄÍCDÓÚEŁŹÔòËıßĐÎAECFÊÇŸŰĐÎŁź
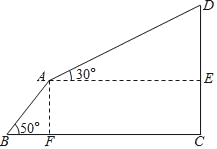
ĄßÔÚÖ±œÇĄśABFÖĐŁŹĄÏB=50ĄăŁŹ
ĄàAF=ABsin50ĄăĄÖ3000ĄÁ0.77=2310ŁŹ
ĄàCE=AFĄÖ2310Łź
ÓÉÌâÒ⣏żÉ”ĂAD=6ĄÁ10ĄÁ60=3600Łź
ĄßÔÚÖ±œÇĄśDAEÖĐŁŹĄÏDAE=30ĄăŁŹ
ĄàDE=![]() AD=1800ŁŹ
AD=1800ŁŹ
ĄàCD=CE+DEĄÖ2310+1800=4110ŁšĂŚŁ©Łź
ŒŽÉœ¶„D”Ğ߶ÈÔŒÎȘ4110ĂŚŁź


 ÌìÌìÏòÉÏÒ»±ŸșĂŸíÏ”ÁĐŽđ°ž
ÌìÌìÏòÉÏÒ»±ŸșĂŸíÏ”ÁĐŽđ°ž ХѧÉú10·ÖÖÓÓŠÓĂÌâÏ”ÁĐŽđ°ž
ХѧÉú10·ÖÖÓÓŠÓĂÌâÏ”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÒŃÖȘ”ăCŁš1ŁŹ0Ł©ŁŹÖ±Ïßy=-x+7ÓëÁœŚű±êÖá·Ö±đœ»ÓÚA,BÁœ”㣏D,E·Ö±đÊÇAB, OAÉϔĶŻ”㣏ÔòĄśCDEÖÜł€”ÄŚîĐĄÖ”ÊÇ_____________.

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄłŒÓÓÍŐŸÎćÔ·ĘÓȘÏúÒ»ÖÖÓÍÆ·”ÄÏúÊÛÀûÈó![]() ŁšÍòÔȘŁ©ÓëÏúÊÛÁż
ŁšÍòÔȘŁ©ÓëÏúÊÛÁż![]() ŁšÍòÉ꣩֟ŒäșŻÊęčŰÏ””ÄÍŒÏóÈçÍŒÖĐŐÛÏßËùÊŸŁŹžĂŒÓÓÍŐŸœŰÖč”œ13ÈŐ”śŒÛʱ”ÄÏúÊÛÀûÈóÎȘ4ÍòÔȘŁŹœŰÖčÖÁ15ÈŐœűÓÍʱ”ÄÏúÊÛÀûÈóÎȘ5.5ÍòÔȘŁźŁšÏúÊÛÀûÈóŁœŁšÊÛŒÛŁłÉ±ŸŒÛŁ©ĄÁÏúÊÛÁżŁ©
ŁšÍòÉ꣩֟ŒäșŻÊęčŰÏ””ÄÍŒÏóÈçÍŒÖĐŐÛÏßËùÊŸŁŹžĂŒÓÓÍŐŸœŰÖč”œ13ÈŐ”śŒÛʱ”ÄÏúÊÛÀûÈóÎȘ4ÍòÔȘŁŹœŰÖčÖÁ15ÈŐœűÓÍʱ”ÄÏúÊÛÀûÈóÎȘ5.5ÍòÔȘŁźŁšÏúÊÛÀûÈóŁœŁšÊÛŒÛŁłÉ±ŸŒÛŁ©ĄÁÏúÊÛÁżŁ©
ÇëÄăžùŸĘÍŒÏ󌰌ÓÓÍŐŸÎćÔ·ʞĂÓÍÆ·”ÄËùÓĐÏúÊÛŒÇÂŒÌáč©”ÄĐĆÏąŁŹœâŽđÏÂÁĐÎÊÌâŁș

Łš1Ł©ÇóÏúÊÛÁż![]() ÎȘ¶àÉÙʱŁŹÏúÊÛÀûÈóÎȘ4ÍòÔȘŁ»
ÎȘ¶àÉÙʱŁŹÏúÊÛÀûÈóÎȘ4ÍòÔȘŁ»
Łš2Ł©·Ö±đÇółöÏ߶ÎABÓëBCËù¶ÔÓŠ”ÄșŻÊęčŰϔʜŁ»
Łš3Ł©ÎÒĂÇ°ŃÏúÊÛĂżÉęÓÍËù»ń”Ă”ÄÀûÈółÆÎȘÀûÈóÂÊŁŹÄÇĂŽŁŹÔÚOAĄąABĄąBCÈę¶ÎËù±íÊŸ”ÄÏúÊÛĐĆÏąÖĐŁŹÄÄÒ»¶Î”ÄÀûÈóÂÊŚîŽóŁżŁšÖ±œÓĐŽłöŽđ°žŁ©
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹÖ±Ïß1ŽčÖ±ÓÚxÖᣏŽčŚăÎȘMŁšmŁŹ0Ł©ŁŹ”ăAŁš©1.0Ł©čŰÓÚÖ±Ïß”Ä¶ÔłÆ”ăÎȘAĄäŁź
ÌœŸżŁșŁš1Ł©”±m=0ʱŁŹAĄä”ÄŚű±êÎȘĄĄ ĄĄŁ»
Łš2Ł©”±m=1ʱŁŹAĄä”ÄŚű±êÎȘĄĄ ĄĄŁ»
Łš3Ł©”±m=2ʱŁŹAĄä”ÄŚű±êÎȘĄĄ ĄĄŁ»
·ąÏÖŁș¶ÔÓÚÈÎÒâ”ÄmŁŹAĄä”ÄŚű±êÎȘĄĄ ĄĄŁź
œâŸöÎÊÌâŁșÈôAŁš©1ŁŹ0Ł©BŁš©5ŁŹ0Ł©ŁŹCŁš6ŁŹ0Ł©ŁŹDŁš15ŁŹ0Ł©ŁŹœ«Ï߶ÎABŃŰÖ±Ïßl·ŐÛ”Ă”œÏ߶ÎAĄäBĄäŁŹÈôÏ߶ÎAĄäBĄäÓëÏ߶ÎCDÖŰșÏČż·Ö”Äł€ÎȘ2ŁŹÇóm”ÄÖ”Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÆœĐĐËıßĐÎABCDÖĐŁŹÒÔABÖĐ”ăEÎȘÔČĐÄŁŹEAÎȘ°ëŸ¶»»Ąœ»CDÓÚ”ăFŁŹ”ăFÇĄșĂÎȘCDÖД㣏ÈôĄÏB=60ĄăŁŹBC=2ŁŹÔòÍŒÖĐÒőÓ°Čż·Ö”ÄĂæ»ęÎȘ_____Łź

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹĄśABCžś¶„”ă”ÄŚű±ê·Ö±đÎȘŁșAŁš4ŁŹ0Ł©ŁŹBŁš©1ŁŹ4Ł©ŁŹCŁš©3ŁŹ1Ł©
Łš1Ł©ÔÚÍŒÖĐŚśĄśAĄäBĄäCĄäÊ襜AĄäBĄäCĄäșÍĄśABCčŰÓÚxÖá¶ÔłÆŁ»
Łš2Ł©ĐŽłö”ăAĄäBĄäCĄä”ÄŚű±êŁ»
Łš3Ł©ÇóĄśABC”ÄĂæ»ęŁź

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄłĐŁœűĐĐĐŁÔ°ĂÀ»Żč€łÌŐбêʱŁŹÓĐŒŚĄąÒÒÁœžöč€łÌ¶ÓͶ±êŁŹŸČâËăŁșŒŚ¶Ó”„¶ÀÍêłÉŐâÏî耳ÌĐèÒȘ60ÌìŁŹÈçčûÓÉŒŚ¶ÓÏÈŚö20ÌìŁŹÊŁÏ”Ä耳ÌÓÉŒŚĄąÒÒșÏŚś24ÌìÍêłÉŁź
Łš1Ł©ÒÒ¶Ó”„¶ÀÍêłÉŐâÏî耳ÌĐèÒȘ¶àÉÙÌìŁż
Łš2Ł©ŒŚ¶ÓÊ©č€Ò»ÌìŁŹĐèÒȘÖ§ž¶č€łÌżî3.5ÍòÔȘŁŹÒÒ¶ÓÊ©č€Ò»ÌìĐèÒȘÖ§ž¶č€łÌżî2ÍòÔȘŁșÈçčûč涚ÔÚ70ÌìÄÚÍêłÉŐâÏî而śŁŹÊÇÓÉŒŚĄąÒÒÁœ¶Ó”„¶ÀÍêłÉÊĄÇźŁż»čÊÇÓÉŒŚÒÒșÏŚśÍêłÉžĂ耳ÌÊĄÇźŁż
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹ”ăP”ÄŚű±êÎȘŁš0ŁŹ2Ł©ŁŹÖ±Ïßy=![]() ÓëxÖ᥹yÖá·Ö±đœ»ÓÚ”ăAŁŹBŁŹ”ăMÊÇÖ±ÏßABÉÏ”ÄÒ»žö¶Ż”㣏ÔòPMł€”ÄŚîĐĄÖ”ÎȘŁš Ł©
ÓëxÖ᥹yÖá·Ö±đœ»ÓÚ”ăAŁŹBŁŹ”ăMÊÇÖ±ÏßABÉÏ”ÄÒ»žö¶Ż”㣏ÔòPMł€”ÄŚîĐĄÖ”ÎȘŁš Ł©

AŁź3 BŁź4 CŁź5 DŁź6
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹ![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() ÎȘŸŰĐΔÄËÄžö¶„”㣏
ÎȘŸŰĐΔÄËÄžö¶„”㣏![]() ŁŹ
ŁŹ![]() ŁŹ¶Ż”ă
ŁŹ¶Ż”ă![]() Ąą
Ąą![]() ·Ö±đŽÓ”ă
·Ö±đŽÓ”ă![]() Ąą
Ąą![]() ÍŹÊ±łö·ąŁŹ”ă
ÍŹÊ±łö·ąŁŹ”ă![]() ÒÔ
ÒÔ![]() ”ÄËÙ¶ÈÏò”ă
”ÄËÙ¶ÈÏò”ă![]() ÒƶŻŁŹÒ»Ö±”œŽï
ÒƶŻŁŹÒ»Ö±”œŽï![]() ÎȘÖ裏”ă
ÎȘÖ裏”ă![]() ÒÔ
ÒÔ![]() ”ÄËÙ¶ÈÏò
”ÄËÙ¶ÈÏò![]() ÒƶŻŁź
ÒƶŻŁź

![]() Ąą
Ąą![]() Áœ”ăŽÓłö·ążȘÊŒ”œŒžĂ룿ËıßĐÎ
Áœ”ăŽÓłö·ążȘÊŒ”œŒžĂ룿ËıßĐÎ![]() ”ÄĂæ»ęÎȘ
”ÄĂæ»ęÎȘ![]() Ł»
Ł»
![]() Ąą
Ąą![]() Áœ”ăŽÓłö·ążȘÊŒ”œŒžĂëʱŁż”ă
Áœ”ăŽÓłö·ążȘÊŒ”œŒžĂëʱŁż”ă![]() șÍ”ă
șÍ”ă![]() ”ÄŸàÀëÊÇ
”ÄŸàÀëÊÇ![]() Łź
Łź
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com