
°ĺŐ‚ńŅ°Ņ‘ń∂Ń≤ńŃŌ
≤ńŃŌ1£ļ»Ű“ĽłŲ◊‘»Ľ ż£¨ī”◊ůĶĹ”“łųőĽ ż…ŌĶń ż◊÷”Žī””“ĶĹ◊ůłųőĽ ż…ŌĶń ż◊÷∂‘”¶ŌŗÕ¨£¨‘Ú≥∆ő™°į∂‘≥∆ ż°Ī.
≤ńŃŌ2£ļ∂‘”ŕ“ĽłŲ»żőĽ◊‘»Ľ ż![]() £¨ĹęňŁłųłŲ żőĽ…ŌĶń ż◊÷∑÷Īū2Ī∂ļů»°łŲőĽ ż◊÷£¨Ķ√ĶĹ»żłŲ–¬Ķń ż◊÷
£¨ĹęňŁłųłŲ żőĽ…ŌĶń ż◊÷∑÷Īū2Ī∂ļů»°łŲőĽ ż◊÷£¨Ķ√ĶĹ»żłŲ–¬Ķń ż◊÷![]() £¨
£¨![]() £¨
£¨![]() £¨ő“√«∂‘◊‘»Ľ ż
£¨ő“√«∂‘◊‘»Ľ ż![]() Ļś∂®“ĽłŲ‘ňň„£ļ
Ļś∂®“ĽłŲ‘ňň„£ļ![]() .
.
ņż»Á£ļ![]() «“ĽłŲ»żőĽĶń°į∂‘≥∆ ż°Ī£¨∆šłųłŲ żőĽ…ŌĶń ż◊÷∑÷Īū2Ī∂ļů»°łŲőĽ ż◊÷∑÷Īū «£ļ2°Ę8°Ę2.
«“ĽłŲ»żőĽĶń°į∂‘≥∆ ż°Ī£¨∆šłųłŲ żőĽ…ŌĶń ż◊÷∑÷Īū2Ī∂ļů»°łŲőĽ ż◊÷∑÷Īū «£ļ2°Ę8°Ę2.
‘Ú![]() .
.
«ŽĹ‚īū£ļ
£®1£©“ĽłŲ»żőĽĶń°į∂‘≥∆ ż°Ī![]() £¨»Ű
£¨»Ű![]() £¨«Ž÷ĪĹ”–ī≥Ų
£¨«Ž÷ĪĹ”–ī≥Ų![]() Ķńňý”–÷Ķ£¨
Ķńňý”–÷Ķ£¨![]() £Ľ
£Ľ
£®2£©“—÷™ŃĹłŲ»żőĽ°į∂‘≥∆ ż°Ī![]() £¨»Ű
£¨»Ű![]() ń‹ĪĽ11’Ż ż£¨«ů
ń‹ĪĽ11’Ż ż£¨«ů![]() Ķńňý”–÷Ķ.
Ķńňý”–÷Ķ.
°ĺīūįł°Ņ£®1£©515ĽÚ565£Ľ£®2£©![]() Ķń÷Ķő™4£¨8£¨96£¨108£¨144.
Ķń÷Ķő™4£¨8£¨96£¨108£¨144.
°ĺĹ‚őŲ°Ņ
£®1£©łýĺ›°į∂‘≥∆ ż°ĪĶń∂®“ŚļÕ![]() Ņ…÷™£¨’‚łŲ»żőĽ ż ◊ő≤ ż◊÷÷Ľń‹ «5£¨»Ľļů÷–ľšĶń ż◊÷2Ī∂ļůłŲőĽ żő™2£¨”…īňŅ…Ķ√BĶń÷Ķ.
Ņ…÷™£¨’‚łŲ»żőĽ ż ◊ő≤ ż◊÷÷Ľń‹ «5£¨»Ľļů÷–ľšĶń ż◊÷2Ī∂ļůłŲőĽ żő™2£¨”…īňŅ…Ķ√BĶń÷Ķ.
£®2£© ◊Ō»ĪŪ ĺ≥Ų’‚ŃĹłŲ»żőĽ ż£¨![]() £¨
£¨![]() £¨łýĺ›
£¨łýĺ›![]() ń‹ĪĽ11’Ż ż£¨∑÷«ťŅŲŐ÷¬Ř
ń‹ĪĽ11’Ż ż£¨∑÷«ťŅŲŐ÷¬Ř![]() °Ę
°Ę![]() Ķń÷ĶľīŅ…Ķ√≥Ųīūįł.
Ķń÷ĶľīŅ…Ķ√≥Ųīūįł.
Ĺ‚£ļ£®1£©°Ŗ![]()
”…‘ňň„∑®‘ÚŅ…÷™£¨’‚łŲ»żőĽ ż ◊ő≤ ż◊÷÷Ľń‹ «5£¨÷–ľš ż◊÷2Ī∂ļůłųőĽ ż◊÷ő™2£¨
°ŗ÷–ľš ż◊÷ő™1ĽÚ6£¨
‘Ú’‚łŲ»żőĽ żő™515ĽÚ565
Ļ īūįłő™£ļ515ĽÚ565£Ľ
£®2£©”…Ő‚“‚Ķ√£ļ![]() £¨
£¨![]()
![]() £¨
£¨
![]() ń‹ĪĽ11’Ż≥ż£¨
ń‹ĪĽ11’Ż≥ż£¨
![]() «11ĶńĪ∂ ż.
«11ĶńĪ∂ ż.
![]() °Ę
°Ę![]() ‘ŕ1°ę9÷–»°÷Ķ£¨
‘ŕ1°ę9÷–»°÷Ķ£¨
![]() .
.
ĶĪ![]() £¨
£¨![]() Ī£¨
Ī£¨![]() £¨
£¨![]() £Ľ
£Ľ
ĶĪ![]() £¨
£¨![]() Ī£¨
Ī£¨![]() £¨
£¨![]() £Ľ
£Ľ
ĶĪ![]() £¨
£¨![]() Ī£¨
Ī£¨![]() £¨
£¨![]() £Ľ
£Ľ
ĶĪ![]() £¨
£¨![]() Ī£¨
Ī£¨![]() £¨
£¨![]() £Ľ
£Ľ
ĶĪ![]() £¨
£¨![]() Ī£¨
Ī£¨![]() £¨
£¨![]() £Ľ
£Ľ
ĶĪ![]() £¨
£¨![]() Ī£¨
Ī£¨![]() £¨
£¨![]() £Ľ
£Ľ
ĶĪ![]() £¨
£¨![]() Ī£¨
Ī£¨![]() £¨
£¨![]() £Ľ
£Ľ
ĶĪ![]() £¨
£¨![]() Ī£¨
Ī£¨![]() £¨
£¨![]() £Ľ
£Ľ
![]() Ķń÷Ķő™4£¨8£¨96£¨108£¨144.
Ķń÷Ķő™4£¨8£¨96£¨108£¨144.



| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ∂‘”ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ![]() ÷–ĶńĶ„PļÕÕľ–őM£¨łÝ≥Ų»ÁŌ¬∂®“Ś£ļQő™Õľ–őM…Ō»ő“‚“ĽĶ„£¨»ÁĻŻ
÷–ĶńĶ„PļÕÕľ–őM£¨łÝ≥Ų»ÁŌ¬∂®“Ś£ļQő™Õľ–őM…Ō»ő“‚“ĽĶ„£¨»ÁĻŻ![]() ŃĹĶ„ľšĶńĺŗņŽ”–◊Óīů÷Ķ£¨ń«√ī≥∆’‚łŲ◊Óīů÷Ķő™Ķ„P”ŽÕľ–őMľšĶńŅ™ĺŗņŽ£¨ľ«◊ų
ŃĹĶ„ľšĶńĺŗņŽ”–◊Óīů÷Ķ£¨ń«√ī≥∆’‚łŲ◊Óīů÷Ķő™Ķ„P”ŽÕľ–őMľšĶńŅ™ĺŗņŽ£¨ľ«◊ų![]() £ģ“—÷™÷ĪŌŖ
£ģ“—÷™÷ĪŌŖ![]() ”Žx÷ŠĹĽ”ŕĶ„A£¨”Žy÷ŠĹĽ”ŕĶ„B£¨
”Žx÷ŠĹĽ”ŕĶ„A£¨”Žy÷ŠĹĽ”ŕĶ„B£¨![]() ĶńįŽĺ∂ő™1£ģ
ĶńįŽĺ∂ő™1£ģ
£®1£©»Ű![]() £¨
£¨
ĘŔ«ů![]() Ķń÷Ķ£Ľ
Ķń÷Ķ£Ľ
Ęŕ»ŰĶ„C‘ŕ÷ĪŌŖ![]() …Ō£¨«ů
…Ō£¨«ů![]() Ķń◊Ó–°÷Ķ£Ľ
Ķń◊Ó–°÷Ķ£Ľ
£®2£©“‘Ķ„Aő™÷––ń£¨ĹęŌŖ∂ő![]() ň≥ Ī’Ž–ż◊™
ň≥ Ī’Ž–ż◊™![]() Ķ√ĶĹ
Ķ√ĶĹ![]() £¨Ķ„E‘ŕŌŖ∂ő
£¨Ķ„E‘ŕŌŖ∂ő![]() ◊ť≥…ĶńÕľ–ő…Ō£¨»Ű∂‘”ŕ»ő“‚Ķ„E£¨◊‹”–
◊ť≥…ĶńÕľ–ő…Ō£¨»Ű∂‘”ŕ»ő“‚Ķ„E£¨◊‹”–![]() £¨÷ĪĹ”–ī≥ŲbĶń»°÷Ķ∑∂őߣģ
£¨÷ĪĹ”–ī≥ŲbĶń»°÷Ķ∑∂őߣģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ň◊őÔŌŖ![]() ”Ž
”Ž![]() ÷ŠĹĽ”ŕ
÷ŠĹĽ”ŕ![]() £¨
£¨![]() ŃĹĶ„£¨”Ž
ŃĹĶ„£¨”Ž![]() ÷ŠĹĽ”ŕĶ„
÷ŠĹĽ”ŕĶ„![]() £¨Ķ„
£¨Ķ„![]() «Ň◊őÔŌŖĶń∂•Ķ„£ģ
«Ň◊őÔŌŖĶń∂•Ķ„£ģ
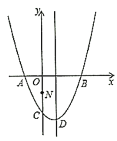
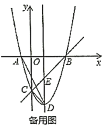
£®1£©«ůŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£ģ
£®2£©Ķ„![]() «
«![]() ÷ŠłļįŽ÷Š…ŌĶń“ĽĶ„£¨«“
÷ŠłļįŽ÷Š…ŌĶń“ĽĶ„£¨«“![]() £¨Ķ„
£¨Ķ„![]() ‘ŕ∂‘≥∆÷Š”“≤ŗĶńŇ◊őÔŌŖ…Ō‘ň∂Į£¨Ń¨Ĺ”
‘ŕ∂‘≥∆÷Š”“≤ŗĶńŇ◊őÔŌŖ…Ō‘ň∂Į£¨Ń¨Ĺ”![]() £¨
£¨![]() ”ŽŇ◊őÔŌŖĶń∂‘≥∆÷ŠĹĽ”ŕĶ„
”ŽŇ◊őÔŌŖĶń∂‘≥∆÷ŠĹĽ”ŕĶ„![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() £¨ĶĪ
£¨ĶĪ![]() ∆Ĺ∑÷
∆Ĺ∑÷![]() Ī£¨«ůĶ„
Ī£¨«ůĶ„![]() Ķń◊ÝĪÍ£ģ
Ķń◊ÝĪÍ£ģ
£®3£©÷ĪŌŖ![]() ĹĽ∂‘≥∆÷Š”ŕĶ„
ĹĽ∂‘≥∆÷Š”ŕĶ„![]() £¨
£¨![]() «◊ÝĪÍ∆Ĺ√śńŕ“ĽĶ„£¨«Ž÷ĪĹ”–ī≥Ų
«◊ÝĪÍ∆Ĺ√śńŕ“ĽĶ„£¨«Ž÷ĪĹ”–ī≥Ų![]() ”Ž
”Ž![]() »ęĶ» ĪĶ„
»ęĶ» ĪĶ„![]() Ķń◊ÝĪÍ__________£ģ
Ķń◊ÝĪÍ__________£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°ŅĹę“Ľ Ę”–≤Ľ◊„įŽĪ≠ňģĶń‘≤÷ý–ő≤£ŃßňģĪ≠Ň°ĹŰĪ≠ł«ļů∑ŇĶĻ£¨ňģ∆Ĺ∑Ň÷√‘ŕ◊ņ√ś…Ō£¨ňģĪ≠ĶńĶ◊√ś»ÁÕľňý ĺ£¨“—÷™ňģĪ≠ńŕĺ∂£®Õľ÷––°‘≤Ķń÷Īĺ∂£© «8cm£¨ňģĶń◊Óīů…Ó∂» «2cm£¨‘ÚĪ≠Ķ◊”–ňģ≤Ņ∑÷Ķń√śĽż «£®°°°°£©
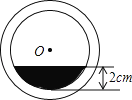
A.£®![]() ¶–©Ā4
¶–©Ā4![]() £©cm2B.£®
£©cm2B.£®![]() ¶–©Ā8
¶–©Ā8![]() £©cm2
£©cm2
C.£®![]() ¶–©Ā4
¶–©Ā4![]() £©cm2D.£®
£©cm2D.£®![]() ¶–©Ā2
¶–©Ā2![]() £©cm2
£©cm2
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņń≥Õ¨—ßņŻ”√ ż—ß÷™ ∂≤‚ŃŅĹ®÷ĢőÔDEFGĶńłŖ∂»£ģňŻī”Ķ„![]() ≥Ų∑Ę—ō◊Ň∆¬∂»ő™
≥Ų∑Ę—ō◊Ň∆¬∂»ő™![]() Ķń–Ī∆¬AB≤Ĺ––26√◊ĶĹīÔĶ„Bī¶£¨”√≤‚Ĺ«“«≤‚Ķ√Ĺ®÷ĢőÔ∂•∂ň
Ķń–Ī∆¬AB≤Ĺ––26√◊ĶĹīÔĶ„Bī¶£¨”√≤‚Ĺ«“«≤‚Ķ√Ĺ®÷ĢőÔ∂•∂ň![]() Ķń—ŲĹ«ő™37°„£¨Ĺ®÷ĢőÔĶ◊∂ň
Ķń—ŲĹ«ő™37°„£¨Ĺ®÷ĢőÔĶ◊∂ň![]() Ķńł©Ĺ«ő™30°„£¨»ŰAFő™ňģ∆ĹĶńĶō√ś£¨≤ŗĹ«“« ķ÷Ī∑Ň÷√£¨∆šłŖ∂»BC=1.6√◊£¨‘ÚīňĹ®÷ĢőÔĶńłŖ∂»DE‘ľő™(ĺę»∑ĶĹ
Ķńł©Ĺ«ő™30°„£¨»ŰAFő™ňģ∆ĹĶńĶō√ś£¨≤ŗĹ«“« ķ÷Ī∑Ň÷√£¨∆šłŖ∂»BC=1.6√◊£¨‘ÚīňĹ®÷ĢőÔĶńłŖ∂»DE‘ľő™(ĺę»∑ĶĹ![]() √◊£¨≤őŅľ żĺ›£ļ
√◊£¨≤őŅľ żĺ›£ļ![]() £¨
£¨![]() )£® £©
)£® £©
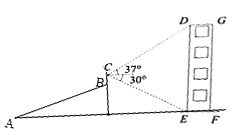
A.![]() √◊B.
√◊B.![]() √◊C.
√◊C.![]() √◊D.
√◊D.![]() √◊
√◊
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕĺō–őAOBC÷–£¨Oő™◊ÝĪÍ‘≠Ķ„£¨OA°ĘOB∑÷Īū‘ŕx÷Š°Ęy÷Š…Ō£¨Ķ„BĶń◊ÝĪÍő™(0£¨3![]() )£¨°ŌABO£Ĺ30°„£¨Ĺę°ųABC—ōABňý‘ŕ÷ĪŌŖ∂‘’Řļů£¨Ķ„C¬š‘ŕĶ„Dī¶£¨‘ÚĶ„DĶń◊ÝĪÍő™(°°°°)
)£¨°ŌABO£Ĺ30°„£¨Ĺę°ųABC—ōABňý‘ŕ÷ĪŌŖ∂‘’Řļů£¨Ķ„C¬š‘ŕĶ„Dī¶£¨‘ÚĶ„DĶń◊ÝĪÍő™(°°°°)

A. (![]() £¨
£¨![]() )B. (2£¨
)B. (2£¨![]() )C. (
)C. (![]() £¨
£¨![]() )D. (
)D. (![]() £¨3©Ā
£¨3©Ā![]() )
)
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
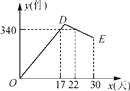
°ĺŐ‚ńŅ°Ņń≥ĻęňĺŅ™∑Ę≥Ų“ĽŅÓ–¬ĶńĹŕń‹≤ķ∆∑£¨ł√≤ķ∆∑Ķń≥…ĪĺľŘő™6‘™/ľĢ£¨ł√≤ķ∆∑‘ŕ’ż ĹÕ∂∑Ň –≥°«įÕ®ĻżīķŌķĶ„ĹÝ––Ńňő™∆ŕ“ĽłŲ‘¬(30Őž)Ķń ‘Ōķ Ř£¨ ŘľŘő™8‘™/ľĢ£¨Ļ§◊ų»ň‘Ī∂‘Ōķ Ř«ťŅŲĹÝ––Ńňłķ◊Ŕľ«¬ľ£¨≤ĘĹęľ«¬ľ«ťŅŲĽś≥…ÕľŌů(»ÁÕľ)£¨Õľ÷–Ķń’ŘŌŖODEĪŪ ĺ»’Ōķ ŘŃŅy(ľĢ)”ŽŌķ Ř Īľšx(Őž)÷ģľšĶńļĮ żĻōŌĶ£¨“—÷™ŌŖ∂őDEĪŪ ĺĶńļĮ żĻōŌĶ÷–£¨ Īľš√Ņ‘Ųľ”1Őž£¨»’Ōķ ŘŃŅľű…Ŕ5ľĢ£ģ
(1)Ķŕ24ŐžĶń»’Ōķ ŘŃŅ « ľĢ£¨»’Ōķ ŘņŻ»ů « ‘™£Ľ
(2)«ůy”Žx÷ģľšĶńļĮ żĻōŌĶ Ĺ£¨≤Ę–ī≥ŲxĶń»°÷Ķ∑∂őߣĽ
(3)»’Ōķ ŘņŻ»ů≤ĽĶÕ”ŕ640‘™ĶńŐž żĻ≤”–∂ŗ…ŔŐž£Ņ ‘Ōķ Ř∆ŕľš£¨»’Ōķ Ř◊ÓīůņŻ»ů «∂ŗ…Ŕ‘™£Ņ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
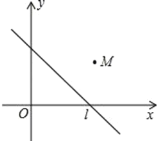
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨“—÷™Ķ„ M Ķń◊ÝĪÍő™£®4£¨3£©£¨Ķ„ M Ļō”ŕ÷ĪŌŖ l£ļy£Ĺ©Āx+b Ķń∂‘≥∆Ķ„¬š‘ŕ◊ÝĪÍ÷Š…Ō£¨‘Ú bĶń÷Ķő™_____£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨“ĽīőļĮ ży1£Ĺkx+b”Ž∑īĪ»ņżļĮ ży2£Ĺ![]() ĶńÕľŌůĹĽ”ŕA£®2£¨3£©£¨B£®6£¨n£©ŃĹĶ„£¨”Žx÷Š°Ęy÷Š∑÷ĪūĹĽ”ŕC£¨DŃĹĶ„£ģ
ĶńÕľŌůĹĽ”ŕA£®2£¨3£©£¨B£®6£¨n£©ŃĹĶ„£¨”Žx÷Š°Ęy÷Š∑÷ĪūĹĽ”ŕC£¨DŃĹĶ„£ģ
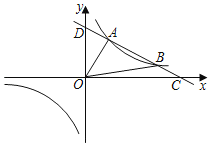
£®1£©«ů“ĽīőļĮ ż”Ž∑īĪ»ņżļĮ żĶńĹ‚őŲ Ĺ£ģ
£®2£©«ůĶĪxő™ļő÷Ķ Ī£¨y1£ĺ0£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com